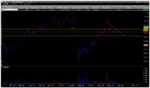
Let us use AIG. For today only, the risk looks as follows.
The Confidence (p<=z) comes in intervals, not a singular value. However, I have been using the bottom value in the interval because it yields a worst case scenario.
P_{0.95} (X>=1) = 61.5% - 97.8%. The true value lies somewhere in the middle. This says I am 95% confidence that the probability of a successful trade is somewhere between 61.5% (worst case scenario) and 97.8% (best case scenario). For this equity today, it is most likely 83.8%. This means that the worst case scenario for an unprofitable trade is 38.5%, i.e., any loss, not necessarily an indicator for the size.
My confidence about the expected return is 95% confident that 61.5% of the trades will be between 2.5% - 8.4%. (1.025 - 1.084). CI about the standard deviation is (0.042 - 0.085).
5% loss = 0.95. 1.025-0.95=0.75/0.84 = 0.892 z-scores.
The area under this curve maps 100% of all probabilities.
=
=
= 0.5
=
The worst case scenario for losing 5%.
95% confident that there is a 18.7% that I could lose up to 5%.
The worst case scenario for losing 10%.
95% confident that there is a 8.1% that I could lose up to 10%.
The worst case scenario for losing 15%.
95% confident that there is a 2.23% that I could lose up to 15%.
The worst case scenario for losing 20%.
95% confident that there is a 0.58% that I could lose up to 20%.