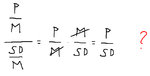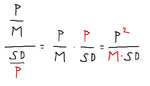my journal 3

[Yamato]

Merkel bei "Wer wird Millionär" - EXTRA 3 - NDR - YouTube

I can't find out what they're saying exactly but it looks interesting. I tried google translate, but some of the translation doesn't make sense.

Soros: Angela Merkel was the creator of the European crisis - YouTube

 

[Yamato]

Too excited to sleep. Either because i am frustrated to have missed a lot of profit or because I am happy to have made some profit (1000 dollars today, which is a lot for me).

Can't sleep. It happens periodically. I might end up writing a lot of things tonight. Or I will turn one of those lectures on, shiller or geanakoplos, and fall asleep.

Watching this show right now:
L'isola dei famosi - Wikipedia, the free encyclopedia

It's pretty pleasant, an island in the caribbean where celebrities (some italians and some foreigners living in italy) have to live together. The people are all right, but the island is beautiful and the filming is very well made.

ISOLA DEI FAMOSI 2011 - Calcoli al tramonto - YouTube


I looked for something on "downside deviation" and found this:

Sortino ratio (versus Sharpe ratio) - YouTube

Bionicturtledotcom again! He's got all the good videos.

What's up with sortino? I know what it is. It's just like the average of all losses. It doesn't make much difference. If there's small losses, they'll even out the big ones.

Actually this is an awesome video, that explains the sortino ratio very clearly. Although I don't like the sortino ratio.

He admits "we are sort of averaging" at minute seven and 14 seconds. But he gave me an idea. Why don't I measure... you see my problem, the reason why I can't use average return over variability or downside risk (which is better) is that I cannot split the contracts. It doesn't matter what the ratio is, because if I am trading Silver and I incur a loss, it will easily blow out my account.

So I need something to tell me not just how good a system is, but how many absolute losses bigger than 400 dollars it has, or whatever is an acceptable level of loss to me. More like 200 dollars.

But then again, 500 dollars is not as bad as 1000 dollars.

So, with an awesome sharpe ratio and lots of money, or with an awesome sharpe ratio and trading stocks, you could reduce the size of your trades, and you'd be fine with those ratios.

But with futures, the size of losses is as important to me as the accuracy of a system.

I might blow out my account due to a high accuracy system making a loss, and instead make money thanks to a lower accuracy system that only loses 200 dollars when it loses.

Otherwise, if I weren't trading futures with a small capital, or if I were able to divide the contracts in as many parts as I want... I could gather all the systems with a sharpe ratio higher than 2, and, for those having losses of 2000, I'd trade one tenth of a contract. For those losing 100, I'd trade 2 contracts... and so on.

That way I'd have a portfolio where the worst losses are 200 dollars.

Instead, unless I want to make no money by trading the only 2 systems that lose 200 dollars per loss, I am forced to have a portfolio in between, that doesn't discard all the good systems trading big futures, but doesn't use them all either, and produces these losses (backtested data):



Which, after some montecarlo resampling in my blender, produce this scenario:


Do you know how wonderful my monte carlo scenario would be if I could split the futures contracts, and have all losses within 500 dollars? I'd make even more money, because i'd be trading twice as many systems, and I'd be going down 1000 dollars at the most.

Let's get to doing this, and screen all the systems I am using by the distribution of losses. Then I might come up with some idea on how to measure them.

[...]

There:


I've listed all the loss by the systems I'm trading in excess of 300 dollars, which I can accept.

This shows very clearly what my problems are: those guys in the picture, those losses. I will print it tomorrow at work, and keep focusing on this. That's been the issue I was not clearly seeing. The contract size.

I never so clearly realized that I have an extra problem compared to most of the financial community and that is why they can use sharpe ratio and other things that I can't use very much. They have a big capital, that doesn't cause them problems with what for me are "big" contracts of most futures. Or they simply trade stocks, and so they can buy as little as they want.

...

By looking at that picture, I see that I could safely trade only one of my systems. GBL_ID_02.

Instead, I trade 13 of them.

It's not a question here about eliminating those losses. I am not discussing about my edge and haven't been working on it for almost a year. It's only a matter of applying the right "loss management" (yeah, remember: I abolished the terms "risk" and "money" management), in order to not blow out my account.

Do I trade the GBL_ID_02 and hope to make 1000 dollars per year, so I can work at the bank for the rest of my life, and then buy a moped when I retire?

Those losses do not show the frequency of the losses smaller than 300, and the frequency and size of wins, but it doesn't matter. The systems are so profitable that my blender shows I have about a 1% chance right now of blowing out my account. Which we could even multiply by 10, and get a realistic 10% chance of blowing out my account.

So I decide it's better to go for it, instead of going for the moped. Yeah, because the alternative for me is not worth it. Your risk also depends on your alternative, and if the alternative is working at the bank anyway, i might as well run a 10% risk of losing the 4000 I invested two months ago.

However, in evaluating a system, I've gotta monitor those losses.

Right now I am so burned out that my brain proceeds very slowly. But it's proceeding in the right direction - I know it.

If I don't get to the point by intelligence, I will get to it by persistence. I will just keep on going in this direction, obsessively: focus on the size of the losses, focus on the size of the losses, focus on the size of the losses...

Of course, the faster my capital grows, the farther away I will get from the possibility of blowing out, and from the concern for the size of the losses.

Then what's 1000 today, will appear as 100, and therefore I would increase - not in the short term but one day - the number of contracts on those showing small losses. And then I could start using the risk metrics used by others. And then I'll take math lessons, finally. And discuss with these teachers... my house will be a scientist hideout.

For now I should just relax and be aware that if I don't do anything - only 1 QG contract still open and then bye bye discretionary trading - I have a... let's even bring it from 1% to 20% chance of blowing out. It can't be higher than that.

 

[Yamato]

developing my own risk metric

The real problem with all these academic papers is that they spend half of the time citing dozens of other people's books (cfr. bull**** author, 2005), and without even explaining one of them clearly (see also Smith, 1989). How can such crap be clear? It's not even making an effort to be clear. It's like writing in code so that just a very few selected people will be able to understand you.

In the next few weeks I will represent a bunch of hypothetical scenarios of trades on a sheet like this one below, I won't waste my time quoting anyone. I'll just reason on my own.

View attachment developing_my_own_risk_metric.xls

There's going to be like about 30 different situations, and I'll find something that answer my needs. I don't care if it's been invented before.

Oh, by the way... according to what I've found out so far, I am dropping profit factor for good (not flushing it down the toilet). I think I may have found something that is better than everything I've seen so far (which is not much).

Here's, for my systems, my own ratio (average monthly profit over standard deviation) on the y-axis and maximum loss (forward-tested and back-tested) on the x-axis:



The better my ratio, the more profitable the system (average monthly profit) relative to its standard deviation. The lower the maximum loss, the better it is for me, given my small capital. This addresses my extra problem of having to trade futures with a small capital. There's oil, gold and silver systems losing up to 20k, but I didn't show them in the chart, because they're not within my reach.

Actually I should fix something, because I'm being able to trade half contracts on EUR and CL, and on the scatter plot this doesn't show. Nah, I won't fix it, because I'd have to change the profit and max loss...it'd be a mess. Let's just remember for CL and EUR that the loss size is half as much.

[...]

**** it. It obsessed me and i could not sleep, so I checked it. What the **** is the difference between standard deviation and average absolute deviation? The only difference is that one gets calculated in a very complicated way, for no reason. It's just like one of those things, like the sharpe ratio.

I wrote a post about it here, being math illiterate, it doesn't say much, but this is all bull****, I am pretty sure:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-48.html#post1788334

So basically, the reason that my system 6 in the previous attached file didn't pick up on the different trades was a mere coincidence (it happens when there are very few points), and avedev is in fact just as good as stdevp (or stdev mother ****er) AND simpler. So now my formula will be monthly profit over average deviation. **** them all...

Here's the chart I plotted of an equity line and the stdevp and avedev excel functions:



Once and for all, they're the same thing - except stdevp is a pain in the ass, let alone the stdev that wants to do the n-1 thing, which is also useless. ****ers.

****!

Wrong again. Stdevp and Avedev get calculated on the trades and not on the equity curve, which is the running total of the trades.

...

Doesn't matter. Still the same:



So, ok, **** standard deviation for good, and let's just use average absolute deviation. What is the standard deviation? It is the average absolute deviation calculated in a stupid way (squaring the deviations, averaging and taking the square root - instead of simply averaging the absolute deviations). This is like -2^2. Everyone says it's easy, and then they get it wrong. Standard deviation is a stupid formula, useless, overcomplex, unnecessary, but everyone uses it. Why? I don't know. They're too busy studying more advanced math to bother with it.

Twelve hours of work and I still can't sleep. Damn. Days go on and on. And they don't end. All my life needed was a sense of some place to go. I don't believe that one should devote his life to morbid self-attention. I believe that someone should become a person like other people.

 

[Yamato]

You know, no one even knows how the sharpe ratio gets calculated correctly anymore. Only sharpe knew it at the start, when he created. But he probably didn't even use it. Did he? These academics... he just wanted to write a brilliant book about it.

You know the average trade on top and the rest on the bottom, plus all the other useless details.

The reason this doesn't work is that, at least the way it's commonly understood, I cannot equally rate a system that makes two trades: 2, -1, with a system that makes six trades: 2, -1, 2, -1, 2, -1. Because the second system makes 3 times as much money. They're just not the same systems. The annualization of profit, all those multipliers do not solve the problem, at least the way they're commonly understood.

Here's what I do instead. I calculate the monthly profit, so I don't care how small the trades are. I just care about the monthly profit. And then I divide it by the average deviation. Because also the variability on the upside matters (cfr.previous post and attachment).

 

[Yamato]

Good stuff here:
Investment Performance Analysis & Risk Management - Value-At-Risk

Value-At-Risk
Value-At-Risk (VaR) answers the question, “How much can the value of a portfolio decline with a given probability in a given time period?”.

[...]

Comparison of VaR and Classical Portfolio Theory

• Risk in portfolio theory = standard deviation of returns, Risk in VaR = maximum likely loss​
• Variance-covariance approach to VaR has the same theoretical basis as portfolio theory. Not so the historical simulation approach and the Monte Carlo simulation approach to VaR.​
• Portfolio theory is limited to market risk, while VaR can be applied to a much broader range of problems (credit, liquidity, operational risks etc.)​
• VaR can better accommodate statistical issues like non-normal returns​
• VaR can be applied for firm-wide risk management and provides better rules than portfolio theory to guide investment, hedging and portfolio management decisions.​
• VaR is not a coherent risk measure ...​

So, goddamn... after calling it "blender" and "shortfall estimator" for a week, I just found out that what it really is, my blender: it is a... Monte Carlo VaR estimator. Lots of hits if I do a search with these terms:
https://www.google.com/search?q=Mon...e7&rls=com.microsoft:en-us:IE-Address&ie=&oe=

Now, this is really the field I am totally comfortable with. I feel at home here. No citing 10 books per page, no summation notation. Just an excel workbook and some macros and functions.

 

[Yamato]

the frustration of discretionary trading is the frustration of being wrong

Missed another 1000 dollars of profit on GBL. So typical. You go through hell for a month, while GBL is going up and down near the top. Then, when it finally turns around to go your way, you exit for a tiny profit, and before your initial target, because you're afraid - after suffering for a month - that it will disappear. And instead you were right, and so, after suffering for a month, because you entered too early, you suffer for another month, out of regrets for not having exited where you had set your target for an entire month. I simply cannot take the frustration of discretionary trading.

But also automated trading is frustrating, because in a similar way, it does not catch the exact reversal, and it does not stay for as long as it should stay. But, being automated, it keeps you from experiencing the pain of being wrong all the time, and from acting while you're frustrated.

That's what my frustration is really all about: I cannot take the uncertainty, and I cannot accept being wrong all the time, and, when you trade, you can't exactly be right, which means you're wrong all the time, and so, if you're like me, you get very upset, and this in turn worsens your trading, and it makes you unprofitable, and frustrated.

[...]

And yet there's something that draws me to it. Like I am drawn to staying up and not sleeping, and that hurts, me, too. Like eating. Like a few other things that are unhealthy and not convenient.

Is it the excitement? What is it? It's so strong an attraction that I couldn't just write here "never again" and "I solemnly swear...", because I've said it so many times, that it's not worth anything anymore.

It'd be like writing that I'll never open up my laptop at night again, which is also unhealthy, for sleeping and your eyesight, but I can't promise stuff like that. Your brain craves excitement, like your stomach craves food. And you can't stop them.

But there's also the strength of maturing, and staying away from temptations. Granted, if someone buys you a cake every day, you might be able to keep yourself from eating it. But there's also tricks, such as killing the person who buys you cakes every day, or telling them to not buy cakes anymore. In the same way, you could stay away from TWS, because if you stare at it, a trading urge will happen. In the same way, you could devise other solutions.

And that's what I am hoping for. I am hoping to mature, and get rid of some addictions. I've done it before, not out of sheer will, but out of such tricks. So, a little bit from maturing and a little bit by being smart about it, I might be able to stop discretionary trading, stop staying up at night, stop eating more than I need to do. Don't get me wrong - I am not fat, but I have those 4 extra kilos that I can't get rid of. Just like I have that extra hour I can rarely sleep at night. But discretionary trading is a whole different thing, because it threatens my overall well-being, my life, my hopes, everything. It's the worst addictions I've ever had to deal with.

 

[Yamato]

2012 Belgian bus crash in Switzerland - Wikipedia, the free encyclopedia

I'm watching online tv. It's the healthiest thing I could ever be doing right now. Better than looking at how much profit I missed, and meditate revenge.

It'd be even better if I could get up, get dressed, and go out. Watch a movie, whatever. I'm sad. And frustrated.

Working on risk metrics is good. But it has nothing to do with staying up all night, engaging in discretionary trading, living an unhealthy life. Actually automated trading makes your life totally healthy as a trader, totally healthy and regular. And it keeps your screen hours to a minimum. It's unbelievable how despite this healthy path I took, I managed to make it unhealthy. Why do I have to always hammer myself in the balls? Maybe my dad taught me that self-sacrifice is the only acceptable way to success, and just sitting and making money from automated trading makes me feel uncomfortable. Mind you, I am not saying I lose out of self-sabotage. I am saying that I am restless out of a sense of guilt, and then restlessness produces negative consequences. This is not the same as saying that I hurt myself to punish myself.

 

[Yamato]

risk metrics study updated

If any of my three readers wants to list me a scenario for me to practice my new risk metric on, let me know. I've updated this file for this purpose:
View attachment developing_my_own_risk_metric.xls

There's a template where you can select a sample of 20 trades (profit and loss, within the realistic scenarios of my systems). It automatically updates a chart with the trades and the equity line, so you can see what your idea looks like.

Furthermore, it automatically updates the ratios I've been studying, to see immediately how they respond to the new scenario, and if they assess it correctly as better or worse than another scenario.

All you need to do is download it, think of some scenario described by 20 trades (it's considered to be one month of trading for any system), and send me the 20 trades, via private message or on a post here. Of course only if it shows something new that I haven't seen.

For example, we've already noticed that Sharpe Ratio and Profit Factor do not measure drawdown, and therefore a system losing 10 times in a row, is the same as a system alternating losses to wins. I excluded this concept from developing anything on it, because drawdown could be a consequence of chance, as for a die. Provided a system is not correlated to the underlying future, I should not measure the drawdown just as i do not measure the drawdown of a die, or a coin. We do not say "this coin has a drawdown of...".

I could have included Return On Investment, but I'd rather keep it separate because if we put too much stuff into my risk metric, we won't know what it measures anymore.

I could have included Correlation to the underlying future, but that, too, for the same reason has to be avoided. Furthermore, correlation is complex to measure because if your system makes money most of the time (as good profitable systems do), and the underlying future, say gold, has been rising most of the time, then there's no way to tell if it's making money because it's good or because it's correlated. You can tell a little, but not as well as for other systems trading futures that have been going up and down like natural gas.

David Bowie - Absolute Beginners - YouTube

 

[Yamato]

Maybe it's good that I'm getting punished like this, and missing out on a profit of 2000 dollars by getting out too early from GBL and NG positions I had been monitoring for a month. This way I won't remember my discretionary trading as a good experience. And even though this won't be enough to put a final end to my discretionary trading, it goes in that direction at least.

Probably if instead of being in trades that meant 5% or 10% of my account (positive or negative), I had been dealing with trades that meant only 2%, I would have made a ton of money by being patient. If instead you're overleveraged, you're too afraid of missing profit and too afraid of losing money to be trading rationally.

It's a long story. And the story will continue as long as I'll have capital. I don't mean new capital - I mean the capital I have on the account right now. So, by "having capital" I only mean "as long as I don't blow out my account".

It's great to be back in the market. Have been back for two months now. I feel like my life has a purpose.

And all my studies and research is much more motivated and concrete than it would be otherwise.

...

I got in touch with my neighbour, former neighbour i mean. Tomorrow I'll call her to go to a movie together.

Taxi Driver - "Dirty movie" scene - YouTube

 

[Yamato]

re-adopting stdevp and re-dropping avedev

I don't know what it is, but I've kept tweaking things and it turned out - it doesn't matter how (can't figure it out right now) - that the stdevp is more sensitive than avedev in measuring changes in the distribution of trades. It seems like avedev is flat all the time.

So I am dropping it again in favor of the good old and berated stdevp. I am talking about using it in my own metric.

I've been wrong because I don't understand all implications of these formulas. But hey, I want to get to the point. I can't go back to college because I want to do things perfectly.

This is the updated version of my file to hypothesize new scenarios:
View attachment developing_my_own_risk_metric.xls

 

[Yamato]

 

[Yamato]

Once Upon A Time in America - Jennifer Connelly - YouTube

 

[Yamato]

Yeah, I am awake again. I can't go to sleep, but tomorrow I definitely have to go to work. I am being haunted by regrets from closing that GBL position early. I've got to turn off all discretionary trading before it kills my brain. I seek and reject the thrill and uncertainty at once, and this whole love-hate relationship is driving me mad, like with a borderline girlfriend I had, where we were breaking up once a week and stayed together for a year like that.

My body is aching from sleep deprivation...

[ Taxi Driver - 1976 ] - "Here's a man who would not take it anymore." - YouTube

 

[Yamato]

4. Portfolio Diversification and Supporting Financial Institutions (CAPM Model) - YouTube

 

[Yamato]

Just who the **** is rating me one day 5 stars and one day 1 star? I had 39 votes for the past month, and just now I went from 2.87 to 2.77, always with the same 39 votes.



So this means some crazy asshole comes here and changes his rating on me, from five to one, and viceversa, every once in a while.

Who the **** are you, asshole? I wish you an immediate death.

If I ever travel to england or something, I gotta remember to register here several times and rate myself five stars, because there's no way trade2win can catch me then, from an internet point or something. Then I'll finally achieve a 5-star rating. Without the risk of being banned.

I need my five-star rating. I am telling you - changes in routine really upset me...

As Good as it Gets- OCD Change in Routine - YouTube

I'm telling you... i'm gonna achieve the 5-star rating. Even if I have to paypal some existing users to rate me five stars.

 

[Yamato]

the right leverage (or right "trade size")

I was reasoning that the right leverage for me is a leverage so that I do not care what happens to a specific trade. That would mean, with the current capital, getting an average win/loss of 300 dollars.

Of course that can't happen for the mentioned reason that futures have a given margin and a given contract size. And so my systems, even some of those presently traded, have wins/losses of up to 1000 dollars (then there's some rare instances of more than that).

This doesn't just increase the variability of returns and the probability of blowing out. It also increases the pressure on me to exit a trade early when it's making money or even keep a system from entering if I am afraid of losing money, thereby missing profit (since the systems are profitable).

This problem will be solved not when all the systems will cause me losses of 300, because, due to contract sizes and systems, this will never happen.

It will instead be solved when I'll have so much capital - three times as much - that losses of 1000 will be equivalent to what losses (or wins) of 300 are now.

Therefore I'd need a capital of 30k to trade in an optimal way. And I'd still have to keep many systems disabled, such as those on silver for example, that could produce wins/losses of several thousands.

Once I'll have that capital, I will triple the contracts of those systems causing me losses/wins of 300, and everything should be balanced in that way.

However, I still have a long way to go in terms of automating this approach. Today I'll have to look into the Shiller lecture I was watching last night, as I was falling asleep, because he might have some exercises for that lecture, that might make CAPM clear to me.

The big obstacle separating me right now from implementing a univocal method for selecting contracts and systems is my math illiteracy.

GOOD CONCISE RECAP
I would divide the problems ahead of me into two groups, both hampered by my math illiteracy:

1) finding a formula for assessing systems individually (cfr. my work on modifying the Sharpe Ratio)
2) finding a formula for assessing systems as a group (or "assessing a portfolio")

For both approaches I have clearly established that maximizing the Sharpe Ratio is NOT the answer, as the Sharpe Ratio does not measure enough things, and among the other things, it does not measure the profitability of a system (intended as Return On Investment).

However, I still have not discarded the CAP Model, because the efficient frontier might not exactly correspond to the Sharpe Ratio (or to the maximization of the Sharpe Ratio).

Here's where I might find the clues about how the CAPM works:
Open Yale Courses | Financial Markets (2008) | Lecture 4 - Portfolio Diversification and Supporting Financial Institutions (CAPM Model)

In the course materials, they've got some tough exercises, but not the solutions:
http://oyc.yale.edu/sites/default/files/problem-set2.pdf

Damn.

The summary of the lecture, on the slides is excellent:
http://oyc.yale.edu/sites/default/files/Lecture04.pdf
http://oyc.yale.edu/sites/default/files/problem-set2.pdf

But still not clear enough for me, and, being math illiterate, I get lost in a sea of summation notation.

I am googling it now, to see if I find something clearer, and I'll manage to find it on excel, too, hopefully.

CAPITAL ASSET PRICING MODEL (CAPM) (Encyclopedia)
Capital Asset Pricing Model (CAPM) Definition | Investopedia

In excel, there's gummy-stuff.org:
www.gummy-stuff.org/Excel/Frontier-data.xls

But it's even harder to understand than summation notation.

Well, at least it's now clearer to me what I do not know.

[...]

I need to look further into gummy-stuff.org:
the Frontier Game

He's done a lot of work, at simplifying things, and yet he's a math professor, so I can trust him.

I need to create a folder with gummy dude and investigate his website inside out.

Also, incredible amount of resources here:
gummy stuff ... about Investing (mostly)

 

[Yamato]

Peter J.Ponzo's Gummy-stuff.org

Awesome website.

Gummy Gone
gummy stuff
Pietro, that's me
gummy stuff ... about Investing (mostly)
(good summaries of Ponzo's resources in the second, third, fourth link)

Here's some of the links I am investigating right now:
CAPM
Efficient Frontier
Efficient Frontier 2
Sortino

Hard stuff made easy by a math professor. This is just the type of stuff I needed.

Now: if I do not learn this inside out, then it's a lack of will on my part. There's no excuse this time.

...

The website is not in perfect order, so you have to go through a labyrinthine path to really find everything, and it's all interesting.

Let's start here:
the gummy Tutorials

In 1993 I retired, after some thirty years of teaching math at the University of Waterloo. I was fifty-nine at the time and would have received a drastically reduced pension, so I transferred thirty years of pension contributions to a self-directed LIF. That meant I had to learn something about investing. I found most things fascinating ... but confusing. When I thought I finally understood the idea behind some financial concept I'd write a tutorial in the hope that others, equally confused, might find something of interest. The tutorials are not meant for professional investors or financial analysts or capital planners or ... whatever.

They're meant for the average do-it-yourself investor who finds much of the literature confusing (including the stuff that's on the Internet).

Just right for me. Now I'll have to go to the movies, but when i come back or tomorrow, I will have to resume and proceed according to this order:
1. http://www.financialwebring.org/gummy-stuff/Efficient-Frontier.htm
2. http://www.financialwebring.org/gummy-stuff/Efficient-Frontier-2.htm
3. http://www.financialwebring.org/gummy-stuff/sortino.htm

Since, thanks to Ponzo, and Shiller, too, I've finally understood that covariance is used for MPT, I might just have found a method to put it all together in an efficient univocal method.

But I have to modify the sharpe first, and that's pretty much done: monthly profit / stdevp of the trades. That's my ratio right now, provided no one writes me any objections with any insights on particular scenarios that make it invalid.

Well, it's not that simple, but if MPT (=CAPM, =efficient frontier) do include the concept of covariance (=correlation), then I might very well use it get my thing together. It's going to take a long time, but it's simple and I'll figure it out.

Maybe one problem will be that covariance or correlation is not that significant for the past, because the trades could have a random order, and so the relationship of the systems with each other could be random, and not a consequence of correlation of any type (that's why I had excluded the assessment of correlation).

Anyway, the path to follow is now clearer than ever. And Ponzo is going to explain those damn formulas to me.

 

[Yamato]

Ok, getting there...

My ratio is going to be monthly return on numerator.

On denominator:
Stdevp of all trades plus margin needed, but this will have to be weighted, because otherwise it will be too important.

But then if margin is weighted... also the trades have to be weighted.

Therefore this is how I'll do it.

average of Return on Investment (using monthly profit)...

I need to think about it more... will resume in the next few posts.

....

No!

After all, a monthly return is not that important in absolute terms, but it could be relativized, by dividing it over the margin, so it'd be the ROI itself.

Then I divide the ROI by the variability and I'm done.

And then I know which system is best, and the only thing to worry about is if I can afford that kind of future in terms of margin required and maximum loss.

All set.

Will finish this when I get back.

[...]

Ok, got back from the movie. This is great. Second movie in a month. Lost money from automated trading but I am relaxed so I am ok with it. Had I been here, I'd have tried to make it back and would have lost even more.

Here's my plan.

While at the movie, I have resolved that I will put on the numerator the monthly profit (because it's simpler to relativize profit that way, since I count the months of forward-testing) divided by the margin required (overnight, since all systems use it, at one moment or another).

On the denominator, I will put variability: either standard deviation (stdevp) or whatever is used by sortino ratio, but probably a modified version, because of the problems I found.

The overall portfolio - I could even skip covariance/correlation - will be optimized (same concept as efficient frontier) when it will achieve the highest possible (portfolio) ratio between ROI and variability. But for this I will need to find a way to uniform all the ROIs, which depend on the margin (different for every system, so I cannot add up the monthly profits, but the ratio of each system's monthly profit to the margin it requires).

But before I focus on portfolio metrics, I need to focus on individual systems' metrics, and so I will keep my scatter plot, where I will keep the maximum losses, because it's the only way to understand - since I don't have an infinite capital - which are the systems that i can afford to trade (regardless of their performance).

[...]

Dude... this Ponzo even explains "second order stochastic dominance", which has been harassing me since I started reading the Bertsimas - Lauprete - Samarov paper:
http://www.financialwebring.org/gummy-stuff/stochastic-dominance.htm

And I still do not understand much. I don't understand his sortino ratio, nor his sharpe ratio, nor his MPT, CAPM... nothing. Actually everything is useful, but he doesn't quite deliver what I had expected.

Well, I achieved something. One little step forward every day.

I obtained the ROI by dividing monthly profit by margin, and then I divided that by stdevp. This is very close to the sharpe ratio. I am satisfied.

One little step at a time. One step at a time. One step at a time. One step at a time.

 

[Yamato]

CAPM Model in 4 Easy Steps - What is Capital Asset Pricing Model Explained (FREE) - YouTube

 

[Yamato]

something ain't right in my ROI to variability ratio

Remember how I said that I would divide ROI by margin, and then the whole thing by the stdevp?

That isn't right, because these two systems should be the same and yet they would not be, if I did things my way:



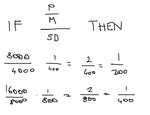
The performance of those two systems is identical, because the one with the smaller margin of 4000 could be turned into the bigger one simply by trading 2 contracts, and THEN the standard deviation would double, because that's how standard deviation works:



So they're identical, precisely because the two different standard deviations are related to the trade size, margin, and profit. And yet they're rated differently by my ratio. This cannot happen.

You know, I was alerted to this by the fact that a mediocre system, such as the GBP_ID_02, scored very well on my scatter plot. And this morning, while reading in the cab, I was wondering why the hell such a poor... not poor but "so so" system, why it scored so well, if I should enable it for trading, or if something was wrong.

So it's now clear that I need to relativize the standard deviation by the margin (or by the profit?), but then if I do that, and get closer to the original Sharpe Ratio, things do work out, but where does the ROI go?



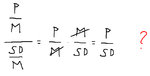
It doesn't seem right either way.

The previous way wasn't right but this doesn't seem to take ROI into account, does it?

Where does the ROI go? Are we still assessing the ROI? Let's check.

[...]

Busy at the office.

Ok, I think I've got it, once and for all.

The ROITVOR ratio
We can't divide SD by margin, because we then lose track of ROI, which comes from Profit divided by Margin.

This is what we have to do:



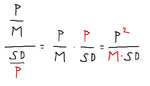
We don't divide SD by margin but by Profit. The number of the numerator, it's clear what it is, and the bigger it is, the better the system is and the bigger our ratio gets. The number on the denominator instead, the bigger it gets, the worse our system gets appraised by the ratio. And if we divide SD by margin, we're not keeping track of ROI any longer, because the two margins (divided by margin, and multiplied by margin) would cancel out... hey, I suck at math, but it's clear that I can't do it and it's clear that with this other formula it works.

Since I suck at math, I had to verify through a practical example:

We have two systems,
1) identical in everything (but with different margins and leverage), and then
2) we have the same two systems where one's margin changes, and then
3) the same two systems where one's SD changes.
The only constant difference is that one system trades a future that's ten times as big as the other one.

[...]

Here's the work on excel:
View attachment two_systems_assessed_with_ROI.to_rel.SD_ratio.xls

and a snapshot:


I think I am on to something. This is excellent work of synthesis - whatever you call it in English. I put together everything I knew in a ratio, which I won't call the "travis ratio", but the... since sharpe said here that his ratio should have been called reward-to-variability ratio, I'm gonna call mine the Reward-On-Investment-to-variability-on-reward ratio (ROITVOR ratio), which is indeed represented by the mentioned equation:



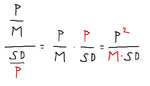
Once I'll get home I'll have to update that excel template file for the tests, because this is a revolutionary change. The ROITVOR ratio is like the Sharpe Ratio (RTV ratio, Reward-To-Variability ratio), but it adds this:

1) it measures profitability
2) it measures profitability based on margin

This is a must for futures traders. I demand a lot of five-star ratings for this invention of mine.

If a system trades 10 times in a year, with a sequence of +2 and -1 trades, the Sharpe Ratio will rate it as well as a system trading 100 times with the same sequence of trades. This is crap as far as I am concerned. The two systems are not the same.

But then, if we measure profitability, we also need to include the margin required to trade the system, and that's where this post comes in. Whatever if anything I did wrong, these are clearly the ruling principles of the whole deal.

If this will work, I will then need to find a way to make it work on a portfolio level, so that I will be able to make theoretical predictions accurate and in line with my blender, the Monte Carlo VaR estimator.

[...]

Back at home and having problems. The multiplying of those two ratios causes the scale to be blown out of proportion. The sharpe ratio did not have this problem at least.

But you know, other than the scale, which can be fixed, what's bothering me increasingly is that the standard deviation is after none other than average loss. Isn't the average loss actually even better than the standard deviation?

Downside risk measures was a good point, and it's haunting me. Sortino and company, I mean.

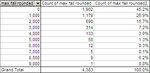
Look, the systems are quite reasonable after all:



I mean the ratio makes sense and brings up the best systems, so I am satisfied. I just mean to make a comparison between max loss, average loss and standard deviation, to see if I can come up with something better.

But other than that, the systems's performance is appraised correctly. For example, in the image above, why is CL_ID_05 three times as good as SI_ID_01, with a score of 36 instead of 12? Because... it's got much more ROI, and all it needs is 2 contracts to make the same money, while still requiring less margin. And also: when it will do that, it will still have less stdevp. Then we'll have to really verify if stdevp is better at measuring downside risk than average loss and max loss are.

Why is NG_ID_04 twice as good as NG_ID_02? Because... with the same investment it makes 25% more profit, and it has 15% less stdevp. So, if and only if, stdevp measures downside risk correctly, then we know this is good stuff, because it compares systems more effectively than sharpe ratio.

[...]

Awesome!!

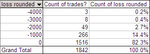
.83 correlation of standard deviation to max losses
.89 correlation of standard deviation to average losses

We can trust standard deviation. So now I just have to fix my scale on the scatter plot and i am set.

And I have to... change developing_my_own_risk_metric.xls" and add these awesome metrics.

[...]

Having problems with the scale. The scatter plot is not clear.