my journal 3

[Yamato]

Worried about a dead-end path... but wrong

You know, all night I was concerned, in my sleep, worried about having taken a dead-end path, with such an unfavorable learning curve that I could get no further.

But then I woke up and I realized that after all these ideas are producing some progress, and not just frustration.

This concept of sharpe ratio not measuring the profitability of a system, in that it doesn't measure the frequency of trading, was a useful concept after all. Yeah, I didn't get much else, at the moment, out of all the work I did in the last few weeks, but this and the resampling concept (with the "shortfall" measurement) were worth it.

Today, I put it into practice on my scatter plot, which does not measure any longer the number of absolute trades, but the number of trades per month:



On the y-axis you see how accurate a system is, and on the x-axis you see how powerful, how frequently it trades. These are just my best systems. I am hiding the others, those with a sharpe ratio below 2 and with less than 1 trade every 2 months.

For example, being NG_ID_04 so young, I hadn't realized that it was so good. So accurate and so profitable, in that it trades 10 times per month. Until now I had the absolute number of trades, and this penalized those systems I had created recently.

I would have felt like adding a bunch of systems, but until I am using an empirical approach, with the resampling, each time I want to add a system, I need to do a lot of work. So I might postpone it for a while longer. Since the previous combination seems to be so balanced.

On the other hand, once again, I feel the need for a thorough theoretical understanding of all the principles governing portfolio theory and the interactions between my ingredients. Let's just say I am getting to know my ingredients a little better, little by little. But what I'd really need is a full immersion into math, with a tutor. I am not talking about high school math anymore, because for that I can use khan academy. I am talking about mathematical finance of course, and everything related to it. I don't know "everything" really, but only what is necessary to keep going in my portfolio theory, the bare minimum. But even the bare minimum, when you're so ignorant, it's hard to identify and learn. So, I am not at a dead end, far from that, but I might get lost. I can go forward, but in so many directions, that, since I don't have enough time to cover them all, I might not have enough time to get where I want to get. Of course if I could have a Chan or Estrada by my side, it would be just a matter of days before I know and understand everything i need, but these guys are not my cousins. I can't write them emails and ask them to solve my problems. And even my cousin is a ****ing asshole anyway.

But you know, the math seeds and concepts are in my head, and something might be growing to my surprise. If I make anything in excess of 15k, I gotta get that math tutoring going.

 

[Yamato]

eureka: replacing sharpe ratio with profit factor and trades with ROI

Ok, I was just now in the bath tub and as usual I could understand things more than anywhere else.

Improving my (empirical) scatterplot, rather than devising a portfolio formula
I figured out the ingredients and I figured out how to put them together, all of them, in one empirical scatter plot.

Agreed, it's not a magic formula like the sharpe ratio that claims to solve all problems, without doing it, but this is just the clearest scatter plot that I ever came up with. I claim less, but I do it right.

The ingredients that must be included in assessing a system's performance are the following, but with two important constraints: time and money invested.

Limits of the sharpe ratio
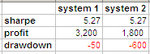
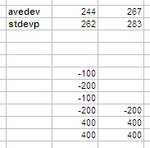
In other words, it doesn't make sense to measure how much money a system makes with a different capital invested than another system, and it doesn't make sense to measure how much money it makes in a different period. Granted? Obvious? Well, guess what: the fabulous sharpe ratio doesn't even see this. If a system makes 2000 and loses 1000, it has the same sharpe ratio as another that makes 200 and loses 100. I see a different return on investment, but sharpe ratio doesn't. And guess what, if (within the same period) a system makes 20 trades in a +200 and -100 in a sequence, or it makes 2000 such trades, sharpe ratio doesn't see that either (except for using stdev instead of stdevp, which causes a tiny difference).

So, these two assumptions are a great improvement compared to how I was doing things before, because I was using sharpe ratio, and yet sharpe ratio ignores them, and so basically it is not an effective tool in comparing different systems: yeah, amazing. I thought it was the ultimate tool to compare different systems - well, I was wrong, along with the whole financial community.

Ingredients, after making those two assumptions
So, given these two assumptions of equal time period and equal capital invested, here's the ingredients:

1) money made, profit
2) variability (zigs zags, ups and downs)
3) correlation, covariance, what have you

And these are just my ingredients for evaluating a specific system - I am not talking about putting them together, because I am far from capable of doing that on a theoretical level, even though I can do it on an empirical level with resampling and shortfall % calculations.

Correlation set aside for now
Despite the fact that these ingredients are not for portfolio (for which I'll keep using my empirical methods for now) but for appraising and comparing systems between one another, despite this, correlation would still be a good quality to assess, but there's a problem. Correlation (or covariance) is not as univocally measured as the rest of the characteristics I've mentioned. Indeed, I mean to find the correlation between the future and the system that trades it, if the system makes money consistently and the future has been rising consistently, such as gold for the last 10 years, or other futures, then my correlation estimate is not accurate. So, if I cannot do it right, I won't do it. I'll do it separately, manually, but it cannot be part of my scatterplot.

Empirical recipe (scatter plot)
Actually I could even come up with a complete formula, like the sharpe ratio, which measures more than the sharpe ratio, but I won't do it, because I want to make money and not write an academic paper that looks good, and is not understandable to anyone other than the other academics. I want to keep the ingredients separate, because I want to look at them, to be aware of them. So I won't use a formula, but I'll keep the ingredients separate in a scatter plot.

Replacing the sharpe ratio with profit factor
The first thing I will do, after all I've said against the sharpe ratio, is to get rid of it, and replace it with the profit factor. What does the sharpe ratio do? In simple words it divides the average profit by the average deviation (forget the rest of the bull**** that makes it look so legitimate and magical). What does profit factor do? Gross profit over gross loss. So the difference is that whereas the sharpe ratio compares money made to deviation (zigzagging, ups and downs), profit factor divides money made over money lost, which is none other than the deviation on the way down, isn't it? So someone tell sortino that he didn't have to invent the sortino ratio but could have gone back to the profit factor. Except profit factor is simpler than sharpe ratio and sortino ratio. So, goodbye academics, for now at least.

Profit factor on x-axis and ROI on y-axis
So, ok, on the y-axis of my scatter plot I will simply put profit factor, which accounts for the accuracy of my system, which was done by sharpe ratio until now. On the y-axis, instead of having the monthly trades, that might not give me a direct idea of the money a system can make, I will put the monthly profit divided by the margin required.

And I am done. It's not a lot, but it's clear. It's the clearest assessment I ever had of my systems.

It's not even accounting for drawdown, but sharpe ratio wasn't either. At least I've added a few things to my scatter plot, and simplified it by getting rid of unclear measurements like the sharpe ratio.

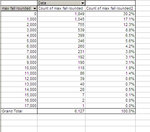
It has one thing missing though: it's the number of trades. I will have to check this manually. Compared to the previous scatter plot I've lost the number of trades:




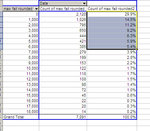
And I've gained Return On Account (monthly profit divided by overnight margin):




There's a lot more systems because, since I am not familiar with it yet, I will allow lower profit factors than I allowed sharpe ratios (after becoming familiar with it, I only allowed systems with sharpe ratios of 2 or above).

The profitability changed a lot of things, and this seems healthy to me. I am getting about twice as much information as I was getting before. For a few more months, there may be some surprising numbers by those systems that didn't trade very much and have very high profit factors.

Let's compare those two charts I posted.

On the first one the 3 most accurate and reliable systems (measured on the y-axis by sharpe ratio) are the same as on the second one (measured on the y-axis by profit factor). So far no surprises, and this applies to all systems, because there's a very strong correlation between sharpe ratio and profit factor (due to how close the concepts are).

The surprise is obviously that, since I added the concept of Return On Investment (ROI), I now notice, on the x-axis, that NQ_ON_02 is almost 4 times as profitable as the other two (due to the margin requirements).

So, on both charts, the most reliable system is NQ_ON_02. The most profitable is, on the second chart, NG_ID_04, which also correctly showed from the first chart, which shows trades per month only because I changed it today from the previous one, that was like this:



And only showed the absolute number of trades, which told me how much the system had been forward-tested.

I am quite satisfied with the present scatter plot. Also, I am quite proud that, despite what everyone says about the sharpe ratio, I just didn't give a **** and went back to the profit factor, which no one ever mentions but that overall is better than sharpe ratio. I am proud of being a free thinker. Almost everyone else would have assumed that, because everyone uses sharpe ratio, it must be the best choice. Despite my insecurity about math, formulas... I still went for what seemed best to me. So, once again, **** you all.

[...]

As i said, this is not a formula that takes care of everything and tells you the overall quality of a system (which sharpe ratio does not do, despite what the financial community seems to think). This is just an empirical chart for me to have an overview of my systems. Having made this premise, can I tell which is my best system by looking at the chart?

NQ_ON_02 and ZN_ON_02 would seem similar in terms of return, but NQ is much more accurate. However, I like ZN better, because it's traded for months and months.

So I guess I am missing the quantity of trades. Can I multiply it? No, nothing can be automated here, because it would not be fair to some of the systems. Just the fact that they were created 3 years ago cannot corrupt their ranking. It should be kept into account, but it cannot be incorporated into the existent rankings.

Ok. Hey, I've done more than enough for today.

[...]

One last thing. I checked the systems traded now, and I noticed that of course they also show on the new scatter plot (I didn't circle them all, but most of them - they're too crowded in there to be recognized):



But this new chart brought to the surface 3 systems that are not being traded - with purple squares around them.

I am not trading the CAD one yet, because it hasn't traded enough yet, and this doesn't show on the chart, but it showed on the chart that I used to have and that is why it never showed. The same applies to the NQ one, which also has problems of margin due to the duration of the trade. But for both, I will add them if I have a little more capital at the next scaling up.

The NG system instead has a lower accuracy and a greater leverage and so I didn't add it, because I could not afford its drawdown, maybe. Or maybe some reason I ignore. Maybe it was too correlated to the other NG systems. Oh, wait, I know. It had a huge drawdown, and the drawdown doesn't show, neither on the sharpe ratio nor on the profit factor (the sequence of trades does not matter to either). The drawdown could be a random thing, and is influenced by the duration of trading. So it should be considered but it cannot be included. Otherwise the systems that didn't trade for long or that got lucky would have an unfair advantage in the ranking.

For sure, whatever looks good on the new scatter plot will be appraised empirically the next time I'll scale up.

[...]

Ok, I am back, willing to work some more.

But before doing the empirical work, is there an equivalent of the sharpe ratio? You know, because they all say "maximize the portfolio sharpe ratio and you're set", which is not true, but I was wondering if I could assess the whole portfolio (from the individual trades or performance metrics) in a way that could anticipate the shortfall calculations I do empirically. If this were possible, then I could save time in the selection process, by first finding the systems in a theoretical way, and then double-checking empirically, but only once I find the best systems.

The first assumption I will make is that we expect no correlation and the order of trades to be random: indeed usually the resampling is worse than the backtesting, so this means random is worse. Maybe this is because I discard those systems that don't fit well together (so in some way I may even be overoptimizing the portfolio).

So, this first assumption makes me set aside once again the ingredient of "correlation" between the systems among each other, or the systems relative to the underlying future they trade.

So all I am left with is finding a method to appraise the portfolio, before the random sampling.

They say that the portfolio with the highest sharpe ratio is the best. Since i threw it out the window and replaced it with the profit factor, now and in the next few days I will have to assess how the profit factor changes as we add systems.

I can start immediately, even though I won't be able to finish this study here.

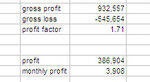
My 120 systems have an average profit factor of 10.3, because there's a guy having a profit factor of 1000 (it has a few trades).

So, I am expecting the combined profit factor to be much lower, because I'll be adding up gross profit and dividing it by the absolute value of gross loss.

And indeed it is: it is 1.08.

Now let's analyze the two best systems or so. And see how profit factor changes if I sum them.

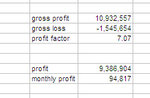
According to profit factor the two best systems are undoubtedly HG_ID_07 with 4 and NQ_ON_02 and 3.5. We can't expect the combined profit factor to be 3.75, because what is weighed is the profit. Whoever made the most profit will affect the combined profit factor the most. This is different from the sharpe ratio, where the bigger system, even if it's better it doesn't matter, because its standard deviation penalizes the sharpe ratio more than its profit does. Here, if the bigger system is better, the profit factor will get closer to its individual value.

Very interesting. I was expecting HG to be the bigger one, because of its big margin and leverage. Instead it's NQ.



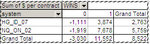
So I am going to divide the total gross profit by the total gross loss and I get 3.81, so this means that since gross profit and gross loss were bigger for NQ, it has been weighed more heavily.

I believe that, unlike for the sharpe ratio, if I maximize the combined (portfolio) profit factor, I will also minimize the shortfall.

But wait, maybe I am wrong.

If I add two systems and one has a huge leverage... no what matters is the size of the trades, not even the gross profit/loss of each system: what matters is the size of its trades. The smaller the better.

If trades are random, as I am assuming, and the drawdown is to be ignored (cfr. assumption a few lines above), then I have to maximize both profit factor and minimize the size of trades at the same time.

In this sense the ROI metric may even be useless or detrimental, because a lot of profit, all other things being equal, may mean bigger losses, and bigger losses mean bigger shortfalls (or whatever it's called). But this is only "all other things being equal", because a system could also achieve a lot of profit (ROI meaning) with many small trades, so ROI is indeed a quality.

Ideally, I would want a bunch of systems with high PF, high ROI, many trades and therefore...

Maybe I should re-enable the number of monthly trades, because that's more indicative... no I won't. I'd probably end up putting it all back as it is now.

Damn.

There's so many variable at play. We're talking about 3 or 4 variables multiplied by a bunch of systems.

Empirically I have now doubts: the way to go is shortfall minimization, and measuring it by % of blowing out probability.

In a theoretical way instead, I am far from figuring out the recipe. And now I'll try to take a break for the rest of the day. This is a challenge that I don't want to quit, so my mind keeps coming back to it.

 

[Yamato]

more ranting against the sharpe ratio

How The Sharpe Ratio Can Oversimplify Risk

When looking to invest, you need to look at both risk and return. While return can be easily quantified, risk cannot. Today, standard deviation is the most commonly referenced risk measure, while the Sharpe ratio is the most commonly used risk/return measure. The Sharpe ratio has been around since 1966, but its life has not passed without controversy. Even its founder, William Sharpe, has admitted the ratio is not without its problems.

[...]

...Remember, as Harry Kat, professor of risk management and director of the Alternative Investment Research Center at the Cass Business School in London, said, "Risk is one word, but it is not one number."

I am going to show an excellent example here, and attach my usual workbook (sheet 6). This ratio, as is recommended by Sharpe himself, should be called "reward-to-variability ratio":
The Sharpe Ratio

I introduced a measure for the performance of mutual funds and proposed the term reward-to-variability ratio to describe it...

And yet it often fails to do just that.

Check this chart out. Two systems are producing some trades in the same period:



Which one do you like better? The one that makes more money with less variability (superior reward to variability) or the one that makes less money with more variability (inferior reward to variability)?

Answer is simple, right? You want to make more money with less variability. But guess what: they have the same sharpe ratio, also known as "reward-to-variability" ratio.



As long as the ratio between zig1 and zag1 is the same as the ratio between zig2 and zag2, for the sharpe ratio the two systems are the same. It doesn't matter if a system achieves more total profit (by trading more) or if a system has less absolute variability (by trading more). These are the same limits as the Profit Factor, but hey, at least the Profit Factor is more modest, it didn't win a nobel prize, and it's calculated much more easily. And finally the sharpe ratio (just as the profit factor) does not care how much money is being invested. So, again, don't tell me that maximizing the sharpe ratio alone can guarantee you jack****. I still haven't figured out much math about all this, but I can understand this much.

I can't believe i wasted so much time with this ratio. No ****. No wonder even sharpe is bothered by it being called "sharpe ratio". It totally got blown out of proportion. It is way overrated and it was not meant to be what it has become.

This is my little file:
View attachment study_on_sharpe_ratio_vs_profit_factor.xls

I cannot believe that with the little math I know I have totally destroyed what the "quants" seem to consider the holy grail. This is total crap. It's just as good as profit factor, if not worse, and it's much more confusing, equivocal, and likely to cause misunderstandings.

Unfortunately, due to the heavy work with the investors, all last year, I've got the sharpe ratio deeply ingrained all over my workbooks. Now, little at a time, I'll remove it. It's a total failure. I can't believe I wasted so much time on it.

Now I'm gonna devise my own ratio. And if I can't, I'll use profit factor in conjunction with some other metrics, two or three (mostly just ROI).

[...]

Recap.

Sharpe ratio with all its fuss, ignores total profit achieved, absolute variability (both depend on frequency of trading, which sharpe ratio doesn't measure), and Return On Investment. I need to incorporate these things into my scatter plot and assessment of my individual systems, because the profit factor ignores those same things.

Return On Investment has already been incorporated. So I need to account for absolute variability ("absolute" to indicate that it ain't just average variability - deviation - relative to average return, and viceversa, which is given by the sharpe ratio). How do I do this?

I have thought of adding the drawdown to the margin requirements for each system. And this is close to being the perfect answer, but:

1) if I have only 5 years of backtesting, or a short period of forward-testing, a system will have a shorter drawdown just because of probability reasons. At the same time its monthly return will not be affected, so it will have an unfair advantage. This means I cannot use maximum drawdown.

2) Maximum drawdown furthermore could be a pure coincidence. It could be luck, random, chance... the fact that three losses happened in a sequence could have nothing to do with the system, but just with chance. Yet another reason to not use maximum drawdown.

By the way maximum drawdown is a concept just as abused, misused and overrated as sharpe ratio is. They're so fashionable, and taught in books and they're so stupid and wrong. "Oh, find the maximum drawdown" and "oh, find the sharpe ratio", but guess what? That's just chance. Maximum drawdown doesn't exist, because it is infinite. It's just a matter of "what drawdown has what probability", and the infinite drawdown has a very small probability (depending on the systems), maybe, but the max drawdown is infinite and if your backtests do not show it, it's just because they're not long enough.

So let's keep going: I cannot use maximum drawdown, but I need to stick in that ROI x-axis measurement something very close to maximum drawdown.

Brainstorming:

1) I can't use drawdown because of what i said.

2) for the same reason (it could be a random event and it's affected by the duration of back-testing or forward-testing), I cannot use maximum loss. The longer the testing, the higher the max loss, and since on the numerator I use the monthly profit, this is an unfair advantage for the systems that have less testing (back or forward).

3) I could use average loss, the only thing left that I can think of. But then a system that screws around a lot, would also have an unfair advantage, because let's say it gets 30 losses, of which one is 100 dollars and the others are 1 dollars. Then another system has 1 loss of 100 and no 1-dollar losses. They'll have the same profit factor (not the same sharpe ratio, interestingly), but one will have a very low average loss and the other one a very high one.

All in all, I have devised a simple method to calculate this thing, too.

I will add to the denominator the highest loss, from both forward testing and backtesting. If I put the two together, I am very likely to get a reasonable estimate, because the years of backtesting are rarely less than 5, so even if the forward-testing period is quite different among systems, this will be compensated by the backtesting.

All set. I will now do the new scatter plot and post it.



Ok, this is it. It can't get much better now.

It measures pretty accurately:

1) Accuracy with profit factor
2) ROI with monthly profit over margin plus max loss (back & forward testing), so it also includes a rating of absolute variability, or real variability... i don't know what to call it - basically not the one by the sharpe ratio

Hey, I am not a mathematician, so I can't put it all together, but it's better than putting it all neatly together and it's wrong.

Much better this thing that I understand, rather than some magic formula which does even less.

From here on, I need a mathematician to tutor me and work with me. I can't go any further, or, without advanced math skills, it will become an intricate mess. Remember, "risk" is one word but it's not one number:
http://www.investopedia.com/articles/07/SharpeRatio.asp

Remember, as Harry Kat, professor of risk management and director of the Alternative Investment Research Center at the Cass Business School in London, said, "Risk is one word, but it is not one number."

 

[Yamato]

shortfall blender estimator



Since I could not do everything theoretically, given that i suck at math still, I basically created on excel a trade blender, with a macro and a bunch of other functions:



I put into the blender all the trades that my systems have been making since I started trading them, and basically the results are pretty good now. No matter how many times I mixed those trades, the likelihood of blowing out is pretty far right now, because I have close to a zero probability of losing more than 3000. I've done it several times. Of course it will never be zero. But, no matter how high it is, I still can say that I have at least a 99% chance of survival. You know what I mean? Even if I happened to mix the trades and get a shortfall that would kill my account, it would still be one trade in 100 trades.

Of course if I stick into the blender the back-tested trades, then I get a pretty good estimate of whether adding a system will improve my chances of survival on top of improving the profit or not. It's a drawdown or shortfall estimator. The back-testing has to be healthy though, because if your system is not built correctly its past trades will not resemble its future trades.

But I cannot be accused nor accuse myself of cheating in any way with forward-testing, because those trades are the trades by the systems that I've enabled and considered the best, so at worst, I can fear that I've been lucky.

So now, I have a tool (the scatter plot) that helps me assess what systems have performed best, and another system to empirically assess if they'll help my portfolio, and I am only lacking the mathematical skills to understand and formulate the concepts that rule a portfolio's performance.

[...]

Ok, there it is. I just found the umpteenth paper, that I'll have to quote as usual. These guys are from MIT... Dimitris Bertsimas, Geoffrey J. Lauprete, Alexander Samarov:
http://web.mit.edu/~dbertsim/www/pa...risk measure- properties and optimization.pdf

It'll tell me if I am using the term "shortfall" correctly. From what I've read so far, we're all dead on target except for their usual academic bull**** and formulas that I'll find for sure and that I won't understand.

Listen to this and tell me if it doesn't remind you what I've been ranting about for days (I marked in red the words that ring a bell and sound familiar):

Abstract
Motivated from second-order stochastic dominance, we introduce a risk measure that we call
shortfall. We examine shortfall’s properties and discuss its relation to such commonly used risk
measures as standard deviation, VaR, lower partial moments, and coherent risk measures. We
show that the mean-shortfall optimization problem, unlike mean-VaR, can be solved efficiently as
a convex optimization problem, while the sample mean-shortfall portfolio optimization problem
can be solved very efficiently as a linear optimization problem. We provide empirical evidence
(a) in asset allocation, and (b) in a problem of tracking an index using only a limited number
of assets that the mean-shortfall approach might have advantages over mean-variance.

The hell with this language... "linear", "convex", "stochastic dominance", etcetera. They're certainly talking about my blender, so let's keep reading.

This is one lovely paper. It's got the working clickable links, too, despite being on .pdf.

Here they go, ranting against markowitz, as I expected:

The standard deviation of the return of a portfolio is the predominant measure of
risk in :nance. Indeed mean-variance portfolio selection using quadratic optimization,
introduced by Markowitz (1959), is the industry standard. It is well known (see Huang
and Litzenberger, 1988 or Ingersoll, 1987) that the mean-variance portfolio selection
paradigm maximizes the expected utility of an investor if the utility is quadratic
or if returns are jointly normal, or more generally, obey an elliptically symmetric
distribution. 1 It has long been recognized, however, that there are several conceptual
di7culties with using standard deviation as a measure of risk

I told you so!

Ok, I'll finish this tomorrow. I don't want to read it now that I'm so tired. This is great, seing eye to eye with people who speak an unknown language and yet I know what they're saying, despite not speaking their language. "Motivated from second-order stochastic dominance"... the world of bull****. Probably these guys don't even trade.

No ****. It's actually a term that means something:
Stochastic dominance - Wikipedia, the free encyclopedia

The other commonly used type of stochastic dominance is second-order stochastic dominance. Roughly speaking, for two gambles A and B, gamble A has second-order stochastic dominance over gamble B if the former is more predictable (i.e. involves less risk) and has at least as high a mean. All risk-averse expected-utility maximizers (that is, those with increasing and concave utility functions) prefer a second-order stochastically dominant gamble to a dominated gamble. The same is true for non-expected utility maximizers with utility functions that are locally concave.

Still don't understand much.

Oh, and here's this, too:
Stochastic dominance - Wikipedia, the free encyclopedia

Portfolio analysis typically assumes that all investors are risk averse. Therefore, no investor would choose a portfolio that is second-order stochastically dominated by some other portfolio. See modern portfolio theory and marginal conditional stochastic dominance.

So I am dead on target.

Hey, how did these guys get so good? Even the guy who wrote this wikipedia entry, I mean: I am not living around people who are capable of even understanding a line of this wikipedia entry.

The academic scientific world is still abundant with bull****, but there's much more substance than in the humanities academic world.

I am really enjoying the intellectual challenge - it's great for once to feel stupid (I am so used to being surrounded by idiots) - but if I can make money with it, it will be that much better.

[...]

I just woke up and i put my blender to work. I mixed the back-tested trades (rather than the forward-tested ones, as I did yesterday - those are much better) of my present 13 systems being traded and I got roughly an 85% chance of survival (shortfall of less than 6000 dollars), if I trade the present 13 systems with the present capital, like in this example.



What happens if I add those two (NG and CAD) that yesterday, on my new scatter plot, did so well?



Like in this example, I get about 83% chance of survival. So let's now see if the profit factor improved nonetheless. It'd be interesting.

Profit factor of prospective 15 systems is 1.48.
Profit factor of presently traded 13 systems is... 1.49.

So yeah, in this case the profit factor might have helped forecast the shortfall estimator.

But, while I was doing this, I just had an another idea. As I said yesterday, I am using on my scatter plot's x-axis a Return On Investment, calculated with monthly profit on the numerator and margin + maximum (back-tested or forward-tested) loss. Since these two systems proved to be worse than I thought, why don't I maximize the impact on the ratio of the maximum loss? It will probably be proportional to the margin anyway. In this way, I make my ratio much more sensitive to shortfall, while at the same time keeping an idea of the margin. Before doing this I will calculate the correlation between maximum loss and margin required, to see if I am right in my assumption.

Yes, I am: 0.72 correlation (with correl function on excel). So I will change my scatter plot to show ROI based on maximum loss.

In the process, I discovered something else, that is interesting. The relationship between the margin and the max loss, for my systems, goes from 0.6 to 7.2. This means that there's cases where your margin is exceeded by the maximum loss, and other cases (the majority) where even the maximum loss is much less than the margin required. This is interesting because the whole concept of margin revolves around the concept of maximum loss.

So, after having delved into this, I can get rid of margin.

And I get this new chart, with ROI given by monthly profit divided by max loss:



And now I can take a break, because I am really proud of the clarity of this chart.

[...]

Ok, let's keep on reading the shortfall paper by those guys from MIT (Dimitris Bertsimas, Geoffrey J. Lauprete, Alexander Samarov):
http://web.mit.edu/~dbertsim/www/pa...risk measure- properties and optimization.pdf

It has a great web design, so to speak, because the footnotes and bibliography references take you to the book by clicking on them. That's how I got to the end of the paper, and found this useful "conclusions":

7. Conclusions
We have shown that shortfall naturally arises as a measure of risk by considering
distributional conditions for second-order stochastic dominance. We examined its properties
and its connections with other risk measures. We showed that optimization of
shortfall leads to a tractable convex optimization problem and to a linear optimization
problem in its sample version. Interestingly, portfolio separation theorems as well
natural definitions of beta can be derived in direct analogy to standard mean-variance
portfolio optimization theory. We showed computationally that the mean-shortfall approach
generates portfolios that can outperform those generated by the mean-variance
approach. Finally, we showed that the mean-shortfall approach can readily address
portfolio optimization problems with cardinality constraints. All these considerations
convince us that we should consider more closely the notion of shortfall in real world
environments.

I'm going to first find the links on the web to some the words I don't know (those that seem most important):
Beta (finance) - Wikipedia, the free encyclopedia

In finance, the Beta (β) of a stock or portfolio is a number describing the relation of its returns with those of the financial market as a whole.[1]

An asset has a Beta of zero if its returns change independently of changes in the market's returns. A positive beta means that the asset's returns generally follow the market's returns, in the sense that they both tend to be above their respective averages together, or both tend to be below their respective averages together. A negative beta means that the asset's returns generally move opposite the market's returns: one will tend to be above its average when the other is below its average.

Ok, my systems have a beta of zero, more or less. I mean, those systems I pick for trading, which are the best ones.

This I found yesterday, and quoted it earlier in this post, but I already forgot what it means:
Stochastic dominance - Wikipedia, the free encyclopedia

The other commonly used type of stochastic dominance is second-order stochastic dominance. Roughly speaking, for two gambles A and B, gamble A has second-order stochastic dominance over gamble B if the former is more predictable (i.e. involves less risk) and has at least as high a mean. All risk-averse expected-utility maximizers (that is, those with increasing and concave utility functions) prefer a second-order stochastically dominant gamble to a dominated gamble. The same is true for non-expected utility maximizers with utility functions that are locally concave.

Then I don't understand the concave-convex thing, and linear optimization even. I really suck.

Yeah, they've got an entry for that as well, but it takes me to whole lot of side entries which I still do not understand, so I can't go any further right now:
Convex optimization - Wikipedia, the free encyclopedia

Convex minimization, a subfield of optimization, studies the problem of minimizing convex functions over convex sets. The convexity property can make optimization in some sense "easier" than the general case - for example, any local minimum must be a global minimum.

The good thing about all these papers is that yes, they're full of bull**** and useless jargon, but 1) they're free and 2) they're not out to rip me off. They're just out to show off their knowledge and intelligence. I am really proud of having gone from the field of people out to rip me off to the field of people trying to impress me with their knowledge and intelligence. Their papers are readily available for free on the web. I spend less and I get more intelligence and information.

Anyway, let's keep reading the rest of the paper. More or less until here, I seem to be on track, even though they're speaking a foreign language to me. I mean, they seem to be on track, because I know what's right, and my blender is right. So far, that's what they're talking about: my blender.

ABBA - Dancing Queen - Bassline - YouTube

[...]

In the References, at the end of the paper, they mention this website:
GloriaMundi.org--Home

I found a good video on it, by the usual bionicturtledotcom (I've mentioned it in previous posts):

Intro to Quant Finance: Value at Risk (VaR) - YouTube

What I almost missed is that gloriamundi.org has an incredible database of portfolio theory articles:
GloriaMundi.org--Documents

Gold mine for portfolio theory. I did a search on "Sharpe" and found many interesting articles:



For example this one:
GloriaMundi.org--Documents--Adjusting for Risk: An Improved Sharpe Ratio

Summary
This paper proposes a new rule for risk adjustment and performance evaluation. This rule is a generalization of the well-known Sharpe ratio criterion, and under normal conditions enables a manager to correctly assess alternative risky investments. The rule is superior to existing rules such as the standard Sharpe rule and the RAROC, and can make a substantial difference in estimates of required returns.

Basically I just found a place where there's a bunch of people who are doing what I am doing, and are telling me all the details about it.

Some good articles that I am saving on my list to read and that I am finding directly from gloriamundi.org or through papers that cite them:
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.201.7815&rep=rep1&type=pdf

We introduce stochastic optimization problems involving stochastic dominance constraints.
We develop necessary and sufficient conditions of optimality and duality theory for these
models and show that the Lagrange multipliers corresponding to dominance constraints are concave
nondecreasing utility functions. The models and results are illustrated on a portfolio optimization
problem.

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.196.3379&rep=rep1&type=pdf

We consider the problem of constructing a portfolio of finitely many assets whose
returns are described by a discrete joint distribution. We propose a new portfolio
optimization model involving stochastic dominance constraints on the portfolio return.
We develop optimality and duality theory for these models. We construct equivalent
optimization models with utility functions. Numerical illustration is provided.

http://www.aorda.com/aod/casestudy/..._ssd/CS_SSD_Portfolio_Optimization_matlab.pdf

This case study finds a portfolio with return dominating the benchmark portfolio return in the
second order and having maximum expected return. Mean-risk models are convenient from a
computational point of view and have an intuitive appeal. In their traditional form, however,
they use only two (or a few) statistics to characterize a distribution, and thus may ignore
important information. Stochastic dominance, in contrast, takes into account the entire
distribution of a random variable. The second-order stochastic dominance is an important
criterion in portfolio selection.

http://www.edge-fund.com/Dowd00.pdf

This paper proposes a new rule for risk adjustment and performance evaluation. This rule
is a generalization of the well-known Sharpe ratio criterion, and under normal conditions
enables a manager to correctly assess alternative risky investments. The rule is superior to
existing rules such as the standard Sharpe rule and the RAROC, and can make a substantial
difference in estimates of required returns.

I just mentioned this one a few lines earlier. But I hadn't found the online pdf.

Hey, this is the price I have to pay: they all talk about "second-order stochastic dominance". Little by little, I will have to get into this language or it's hopeless.

And finally here's one more... that looks excellent from the abstract (just by reading the abstracts I am learning a lot about the subject):
GloriaMundi.org--Documents--Beyond Sharpe Ratio: Optimal Asset Allocation with Asymmetrical Performance Ratios

As the assumption of normality in return distributions is relaxed, the classic Sharpe ratio becomes a questionable tool for ranking risky projects, so in recent years several alternatives have been proposed in the literature. Some of these redefine the risk measure, such as the Gini ratio, the Mean Absolute Deviation (MAD) ratio, the Stable ratio, the Mini-Max ratio, the Sortino-Satchell ratio, the VaR and STARR ratios. Other indexes such as the Farinelli- Tibiletti ratio and Generalized Rachev's ratios redefine both the risk and the reward measuring, specifically, they are based on a proper upper/lower partial moments (measuring the deviations from the benchmark) and proper quantile measures. The individual asymmetrical sensitivities towards the extreme events are captured by a proper order of the moments involved. In the paper at hand the portfolio optimization is obtained through the above mentioned eleven performance ratios and a comparison in asset allocation aid system is carried out. We refer to the exponential weighted moving average approach (EWMA) as the forecasting model for the expected returns and the covariance matrix. Backtesting confirm the Generalized Rachev ratios and the Farinelli-Tibiletti ratios outperformed in forecasting ability with respect to the remaining ratios under consideration.

Man, I agree pretty much with everything they say, within the 50% that I understand. What still puzzles me is how on earth can these guys write (and read!) all these papers if, as i am confident, few of them trade. I don't understand where they find the motivation. And if they trade, and make money, I still don't understand where they find the motivation. So I don't understand how anyone could find the motivation to do all the things these guys are doing. For the sake of academics? Why?

Ok, maybe this is a partial answer:



They make them write 200 pages on portfolio theory to get a ph.d.? Could that be the only reason. If that's why, it really sucks, because I am not going to get very useful information. No wonder these papers seem filled with bull****. If they are a "requirement"... the word speaks for itself. I remember when I was in school, and I had to write some bull**** theses for French or similar. I was required to write bibliography and footnotes... what a waste of energy. Nothing done in a situation like that can ever be valuable. Bleah... disgusting. Hopefully by sifting through this bull****, I'll find something good. Anything beats going through the popular financial literature marketers' bull****.

Anyway, let's keep reading.

While looking for the previous pdf, which I could not find, I found this other one:
http://ect-pigorsch.mee.uni-bonn.de...-Serrano_Index_to_Performance_Measurement.pdf

We propose a performance measure that generalizes the Sharpe ratio. The new
performance measure is monotone with respect to stochastic dominance and consistently
accounts for mean, variance and higher moments of the return distribution.
It is equivalent to the Sharpe ratio if returns are normally distributed. Moreover,
the two performance measures are asymptotically equivalent as the underlying
distributions converge to the normal distribution. We suggest a parametric and a
non-parametric estimator for the new performance measure and provide an empirical
illustration using mutual funds data.

I am still puzzled by the concept of "stochastic dominance" which all these guys are using.

Wow. After registering and an odyssey, I managed to download the previous paper from here:
Academia.edu - Share research
Despite the weird last names, these guys are probably all Italians: Farinelli-Ferreira-Rossello-Thoeny-Tibiletti. Probably they're from northern Italy so sometimes their last names don't sound italian.

Actually the exact academia.edu link is here:
Academia.edu | Cookies Required

But it'll ask you to register so it's no good. It's an odyssey to register.

Ok, now I'll read a bit more in that initial shortfall paper and then I'll stop for the day.

I was on page 2 of this paper by Dimitris Bertsimas, Geoffrey J. Lauprete and Alexander Samarov:
http://web.mit.edu/~dbertsim/www/pa...risk measure- properties and optimization.pdf

Asymmetric return distributions make standard deviation an intuitively inadequate risk measure because it equally penalizes desirable upside and undesirable downside returns. In fact, Chamberlain (1983) has shown that elliptically symmetric are the only distributions for which investor’s utility is a function only of the portfolio’s mean and standard deviation.

Berating the sharpe ratio and standard deviation... music to my ears.

Motivated by the above difficulties, alternative downside-risk measures have been
proposed and analyzed in the literature (see the discussion in Section 3.1.4). Though
intuitively appealing, such risk measures are not widely used for portfolio selection
because of computational difficulties and problems with extending standard portfolio
theory results, see, e.g., a recent review by Grootveld and Hallerbach (1999).

This paper is just perfect for me. Tomorrow I'll print it at work. I'm done for today, also because I won't be able to modify this post for much longer.

I just removed from my signature Shiller and Geanakoplos (their lectures), because as I specialize in portfolio theory more and more, they have become less relevant. You know what I mean? They lecture on CAPM and markowitz, so they have become obsolete as far as I'm concerned. I am now into the branch that says sharpe ratio and CAPM are not good enough. Until today I thought I was the only one saying this, and instead within the last 24 hours I managed to find a dozen papers critical on sharpe ratio and attempting to find something better. If people criticize the sharpe ratio, at least they know it, so reading their work is better than listening to the lectures of those (Shiller and Geanakoplos) who just lecture on CAPM and such. That's why I removed them. Also, because I need priorities, as I can't do everything.

 

[Yamato]

shortfall blender findings

Pretty simple. I don't understand the formulas nor the concepts completely, but the blender speaks pretty clearly: shortfall is minimized by increasing the profit factor, and portfolio profit factor is increased by adding systems that have a profit factor higher than the present portfolio profit factor.

However, I now realize that this requires some additional remarks and additional thinking.

You see, this may have happened just because of the systems I've been adding - I was wondering. But maybe not... because ok let's say you add a system that makes 2 trades. One trade adds 10 million dollars, and the other trade loses 1 million dollars. Of course we do not know which trade will come first (in the future). The profit factor is huge, 10/1= 10. Adding this system will greatly affect the portfolio profit factor, improving it and bringing it close to 10, because my other systems make very little compared to this new hypothetical system.

Yet will shortfall benefit from it?

Let's see.

By the way, after testing a little bit with the blender, I removed one of my 13 systems, because it worsened shortfall.

Oh, ok: I can answer the question above by using the blender again. But my prediction is that... if we come across the 10 million dollars win first, the probability of blowing out becomes zero (so to speak) and if we come across the 1 million dollars loss, then the blowout is guaranteed, but hey, that is only one chance in 4000 trades, because there's the other trades as well... let's just test it.

...

Terrible discovery.

This is what happens to the metrics of the portfolios.

Old portfolio:


Portfolio with new hypothetical super-system:


So far everything would seem to be according to plans. The problem is when the 1 million dollar loss hits the equity curve. The portfolio tends to have an average chance of 50% to blow out my small account of 10k.

Now I better make sense of this, because otherwise it means my foundations for the blender go down the toilet.

Ok, if the 10 millions win hits the equity line before the 1 million loss, I never blow out, clearly. Right? Wrong.

Wrong, because shortfall is the fall if I start trading on any given day, so the fact that there's 10 millions made before I start, doesn't make any difference. The fall will be the same.

Let's simplify it. Let's say I can start on any of 100 trades. And one of those trades is a win of 10 millions and another one of those trades is a loss of 1 million. And the rest of the time I just go up and down peanuts, and none of those other trades can blow out my account.


How the loss would wipe me out (increasing % of blowing out as the loss is postponed)If the loss happens on trade 1 of 100, then I only have a 1% chance of blowing out. But the more the loss is postponed, the more are the blowing out days, correct? If it happens on day 100, no matter what I do in the meanwhile with my other mickey mouse trades, i will blow out, because the big loss will wipe me out on the last day. So, recapitulating, if the loss happens on trade 1, I have a 1% chance of blowing out and if it happens on the last day I have a 100% chance of blowing out. This explains why my blender told me that I have more or less a 50% chance of blowing out (depending on how many times I blended things, I got results between 0% and 100%).

How does the win affect the shortfall?
But let's not forget that we added a system that has a profit factor of 10 and that it also has the other trade, a win, showing a profit of 10 million dollars. How does the win interact with the loss? Why doesn't it show on the blender findings?

Ok, if the loss happens on trade 30, then I will have a 30% chance of blowing out - all the trading sequences starting before it (on all the 30 previous trades) will suffer from the 1 million dollar loss and blow out my account.

Can I get the win to affect this adverse probability?

If the win happens on trade 1, all the 30 sequences starting after that trade and before the loss, will still experience the blowing out shortfall.

If the win happens on trade 15, don't i at least rescue the 15 trades before it?

Let's check.

Correct! I only get a 15% chance of blowing out. This is really complex, empirically. And the formulas... I can't figure them out.

What happens if the win happens after the loss?

Nothing, I predict, because all that mattered to my trading sequences starting on any of the 100 trades/dates, is that those starting before the loss, were going to blow out, and those starting afterwards didn't care.

So but doesn't it count that you could make 10 millions due to that win? Nope, because here we're not calculating your chance of blowing out if you start on the first trade, but your chance of blowing out by starting to trade on any of those 100 trades.

The win only affects the probability if it takes place before the loss. And it has the biggest impact if it happens on the trade right before it, thereby reducing the chance of blowing out to 1%.

The loss will tend to have 50% of trades before it (on average), therefore with that alone we have a probability of 50% to blow out. But then win will tend to be before the loss 50% of the time, and on average it will spare half of those trade sequences from blowing out. Because if it's on trade 1, it doesn't make a difference. And if it's right before it, it reduces the chance of blowing out to 1%.

So, as a consequence and recapitulating what I just said, the average probability of blowing out is 25%, after adding a new system with a profit factor of 10.

This is quite shocking and counter-intuitive and not in line what I was expecting.

Unlike what I said at the start, adding a system with a higher profit factor while it increase the overall profit factor, it decreases the likelihood of survival.

So maybe I have to discard profit factor, but first I'll have to check if sharpe ratio is immune from this problem.

Nope. Just the same problem on sharpe ratio. So i'll keep the simpler one.

But this is telling me that I have to understand what ingredient minimizes my shortfall.

If it's not an increased profit factor, it might simply be the size of the individual falls I am adding.

As simple as that: what improves my portfolio is the size of the falls.

Overall profit is already taken care of, accuracy is taken care of... all that's left to be taken care of is something to assess the size of the falls.

As we said, average fall is not good, because an average is an average, and a system could have a lot of losses, helping that average.

So we cannot count on an average.

At the moment I am using the maximum fall, but that's not enough, because I also want to know the frequency of the big falls.

I need to assess the losses, to obsess about them... I'll sleep on it. In a while.

We don't care how many they are. We don't care about their average.

Let's analyze the losses by ng_id_04 for example:

A bunch of them over 500:
-1616
-1406
-1086
-956
-886
-816
-776
-766
-686
-656
-646
-626
-616

A bunch under 500, that we don't care about:
-476
-476
-446
-416
-416
-406
-346
-306
-286
-266
-246
-236
-196
-196
-186
-176
-166
-156
-116
-16
-16

Oh wow... the three biggest losses is indicative. How about we average the 3 biggest losses.

Hmm... too complex.

I'll keep thinking.

However, what is clear now is that the profit factor more or less can tell us the good systems, but adding a system with a higher profit factor is not a guarantee of lowering the shortfall.

What matter in doing that is to add a (profitable) system that has small losses. Of course if I weren't trading futures, but stocks, I could solve this problem by changing the size of the investment in a system. And I'll be able to do this with futures if my capital will be above 200k.

But now I can't do it. And i have to find profitable systems that have small losses.

Actually let's do this immediately.

Let's find those systems and see if shortfall is improved.

I'll do this by finding the profitable systems that have a low gross loss.

NQ_ID_02
JPY_ID_04
GBL_ON_01
GBP_ID_02

Those are the four I might try to add and get away with. I'll do it now.

As expected, the profit factor acutally decreased a little bit, because they are not as good, but I am counting on the fact that they add profit, while having small losses. This should decrease the shortfall, and increase the survival rate from the average of 97%.

It did!

I will enable them right away. At least the best ones:

NQ_ID_02 - ok
JPY_ID_04 - discarded
GBL_ON_01 - discarded
GBP_ID_02 - discarded

I'll enable one of them. I discarded the others for various reasons. Not just that they weren't good.

Ok, enough for today. Hopefully I'll wake up tomorrow and be able to go to work, but not on time. I want to go at about 12, and stay there only 3 hours.

[...]

Still awake.

Amazing how the paper I've been reading addresses exactly the questions I am having as I go along in my practical approach (since I am not a mathematician):
http://web.mit.edu/~dbertsim/www/pa...risk measure- properties and optimization.pdf

Motivated by the above difficulties, alternative downside-risk measures have been
proposed and analyzed in the literature (see the discussion in Section 3.1.4). Though
intuitively appealing, such risk measures are not widely used for portfolio selection
because of computational di7culties and problems with extending standard portfolio
theory results, see, e.g., a recent review by Grootveld and Hallerbach (1999).
In recent years the :nancial industry has extensively used quantile-based downside
risk measures. Indeed one such measure, Value-at-Risk, or VaR, has been increasingly
used as a risk management tool (see e.g., Jorion, 1997; Dowd, 1998; Du7e and Pan,
1997). While VaR measures the worst losses which can be expected with certain
probability, it does not address how large these losses can be expected when the “bad”,
small probability events occur. To address this issue, the “mean excess function”, from
extreme value theory, can be used (see Embrechts et al., 1999 for applications in
insurance). More generally, Artzner et al. (1999) propose axioms that risk measures
(they call them coherent risk measures) should satisfy and show that VaR is not a
coherent risk measure because it may discourage diversi:cation and thus violates one
of their axioms. They also show that, under certain assumptions, a version of the mean
excess function, which they call tail conditional expectation (TailVaR), is a coherent
measure (see Section 3.1.5 below).

When they say "Motivated by the above difficulties..." it seems like I am the one who said, when, a few lines earlier, I was saying:

I need to assess the losses, to obsess about them... I'll sleep on it. In a while.

We don't care how many they are. We don't care about their average.

Of course I don't have their refined language, knowledge, intelligence. I am ok with being modest. If I am not dealing with the usual idiots (that I meet around me all the time), but with mathematicians, I am ok with acknowledging that someone else is more intelligent, cultured, anything.

Our goal in this paper is to propose an alternative methodology for defining,
measuring, analyzing, and optimizing risk that addresses some of the conceptual
difficulties of the mean-variance framework, to show that it is computationally tractable
and has, we believe, interesting and potentially practical implications.

Wow... gee... everything i've been saying in my last ten posts. Sharpe is not good enough, so let's find something better. It's funny. I would have never thought that I could find this in here, in an academic paper. I thought these guys looked down on trading. It's like... as if you were playing soccer, and went through coaches, friends, magazines... everything... and then, after you finetune your searches on google, you end up finding out that they teach the best soccer in a university.

The key in our proposed methodology is a risk measure called shortfall, which
we argue has conceptual, computational and practical advantages over other commonly
used risk measures.

Now is the time I'll find out if I am misusing the term "shortfall" and if instead of it, i shouldn't just use "falls" or "decline in the equity line"... you know? I wouldn't want to misuse a term like that. It would be a shame and an insult to their work.

It is a variation of the mean excess function and TailVaR mentioned
earlier (see also Uryasevand Rockafellar, 1999). Some mathematical properties of the
shortfall and its variations have been discussed in Uryasevand Rockafellar (1999), and
Tasche (2000).

Well, well, this is not enough to realize what they mean by "shortfall".

We propose a natural non-parametric estimator of shortfall, which does not rely on any assumptions about the asset’s distribution and is based only on historical data.

Hey, this sounds precisely like what my blender/shortfall estimator is. Empirical crap basically.

Together with observations in item 3. above, this also importantly
implies that the mean-shortfall optimization may be preferable to the standard
mean-variance optimization, even if the distribution of the assets is in fact normal
or elliptic, because in this case it leads to the e7cient and stable computation of
the same optimal weights and does not require the often problematic estimation of
large covariance matrices necessary under the mean-variance approach.

Yeah, I remember watching a video about it:

Optimum Portfolio Weights for Maximum Sharpe Ratio: Excel - YouTube

Yeah... you maximize the sharpe ratio, through very complex formulas, potentially littered with mistakes, and then what? The beauty of the sharpe ratio was that it was very simple - despite not being very efficient. Then, along the years, they added so much garbage to it, that it is now neither simple nor efficient.

In Section 6, we present computational results suggesting that the e7cient frontier
in mean-standard deviation space constructed via mean-shortfall optimization outperforms
the frontier constructed via mean-variance optimization. We also numerically
demonstrate the ability of the mean-shortfall approach to handle cardinality
constraints in the optimization process using standard linear mixed integer programming
methods. In contrast, the mean-variance approach to the problem leads to a
quadratic integer programming problem, a more di7cult computational problem.

I am really amazed that I am still following somehow what they're saying despite the language they use, which I totally ignore.

When the joint distribution of returns R is multivariate normal, mean-variance portfolio
selection is consistent with expected utility maximization in the sense that given a
:xed expected return, any investor with utility function in U2 will prefer the portfolio
with the smallest standard deviation. This means that in this case standard deviation is
the appropriate measure of risk simultaneously for all utility functions in U2. The same
is true for elliptically symmetric distributions. However, for more general distributions,
variance looses this property...

Still following what they are saying, at least enough to keep reading.

Ok, on page 5 they start with the formulas. And now I am really lost, but I will choose to keep reading and skip the formulas.

Ok, after being lost for the entire page 5, I have now reached page 6, and will continue tomorrow, from here:
"Properties of shortfall".

Let's just do one tiny last thing.

Read more: Shortfall Definition | Investopedia

The amount by which a financial obligation or liability exceeds the amount of cash that is available. A shortfall can be temporary in nature, arising out of a unique set of circumstances or it can be persistent, in which case it may indicate poor financial management practices. Regardless of the nature of a shortfall, it is a significant concern for a company, and is usually corrected promptly through short-term loans or equity injections.

Oh wow, I've been totally abusing the term, according to this investopedia entry above.

But this says a whole different thing:
Expected shortfall - Wikipedia, the free encyclopedia

Expected shortfall (ES) is a risk measure, a concept used in finance (and more specifically in the field of financial risk measurement) to evaluate the market risk or credit risk of a portfolio. It is an alternative to value at risk that is more sensitive to the shape of the loss distribution in the tail of the distribution. The "expected shortfall at q% level" is the expected return on the portfolio in the worst % of the cases.

Wow, awesome. This totally matches what I've been doing and puts it much more clearly than I've read it anywhere else.

Wait, it also says:

Expected shortfall is also called conditional value at risk (CVaR), average value at risk (AVaR), and expected tail loss (ETL).

So let's find that on investopedia:
Conditional Value At Risk (CVaR) Definition | Investopedia

A risk assessment technique often used to reduce the probability a portfolio will incur large losses. This is performed by assessing the likelihood (at a specific confidence level) that a specific loss will exceed the value at risk. Mathematically speaking, CVaR is derived by taking a weighted average between the value at risk and losses exceeding the value at risk.

Once again, this is not what I am doing, at all. I am much closer to monte carlo sampling then.

Monte Carlo Simulation Definition | Investopedia

A problem solving technique used to approximate the probability of certain outcomes by running multiple trial runs, called simulations, using random variables.

I've gotta do a google search with both terms in it:
https://www.google.com/search?q=mon...e7&rls=com.microsoft:en-us:IE-Address&ie=&oe=

There it is! Perfect hits from this search:
RiskMetrics - Wikipedia, the free encyclopedia

All the hits from this search are great, but I'll stop on the first one because it sums it all up. I can't even quote it because it is all good.

All right, I'll quote a part of the wikipedia entry:

Market modelsRiskMetrics describes three models for modeling the risk factors that define financial markets.

[edit] Covariance approachThe first is very similar to the mean-covariance approach of Markowitz. Markowitz assumed that asset covariance matrix can be observed. The covariance matrix can be used to compute portfolio variance. RiskMetrics assumes that the market is driven by risk factors with observable covariance. The risk factors are represented by time series of prices or levels of stocks, currencies, commodities, and interest rates. Instruments are evaluated from these risk factors via various pricing models. The portfolio itself is assumed to be some linear combination of these instruments.

[edit] Historical simulationThe second market model assumes that the market only has finitely many possible changes, drawn from a risk factor return sample of a defined historical period. Typically one performs a historical simulation by sampling from past day-on-day risk factor changes, and applying them to the current level of the risk factors to obtain risk factor price scenarios. These perturbed risk factor price scenarios are used to generate a profit (loss) distribution for the portfolio.

This method has the advantage of simplicity, but as a model, it is slow to adapt to changing market conditions. It also suffers from simulation error, as the number of simulations is limited by the historical period (typically between 250 and 500 business days).

[edit] Monte carlo simulationThe third market model assumes that the logarithm of the return, or, log-return, of any risk factor typically follows a normal distribution. Collectively, the log-returns of the risk factors are multivariate normal. Monte Carlo simulation generates random market scenarios drawn from that multivariate normal distribution. For each scenario, the profit (loss) of the portfolio is computed. This collection of profit (loss) scenarios provides a sampling of the profit (loss) distribution from which one can compute the risk measures of choice.

I guess that I use both historical and monte carlo simulation, after noticing the same problem that i marked in red. Furthermore, the normal distribution is actually better than the distribution that shows in my systems, so I'll use the normal one. In other words, I am expecting the losses from my systems to be random, rather than to offset one another, and is usually the case when I pick a portfolio of systems (for whatever reasons, inversely correlated, or over-optimization).

 

[Yamato]

shortfall estimator with investors' portfolio

As you remember in September the investors and I interrupted trading my systems because they exceeded what we thought would be the "max drawdown", a term which doesn't make sense to me any longer, because the max drawdown can be infinite and it's just a question of probability of it happening.

In September we lost 47k and then we stopped (mostly we lost the profit made in the previous year).

Now, let's see how the shortfall estimator (blender) i made would have estimated our probability of that scenario. It's a simple test, and then I'll go back to sleep.

[...]

Ok, done:



The worst, after running several tests, is 33k. Instead we lost 47k.

This tells me that the shortfall estimator cannot account for:

1) correlation between the systems (losses happening at the same time)

2) systems performing worse in the future than in the past.

In other words, the shortfall estimator tells me that if those trades i fed him were randomly distributed, then my chance would be 99.99% of not blowing out. But those trades did not happen in a random order (correlation problem), and those trades did not happen altogether (back-testing vs forward-testing problem), because worse trades happened instead.

By choosing systems from the forward-tested sample, I partly avoid underperformance, and by choosing fewer systems, I can choose better ones, and that are not as correlated between each other, and so basically my shortfall estimator is more in line with what will happen.

I am satisfied. We underestimated the drawdown simply because 1) we did not pick the systems based on forward-testing but in many cases we trusted back-testing, and they instead underperformed. Then 2) we did not choose the best of the best, since we chose so many for the sake of diversification (but then they were correlated). And 3) because by choosing so many systems (49 systems on 16 futures, some of which correlated), we ended up choosing systems that were correlated.

By choosing around ten systems, I managed to choose
1) systems that are better performing overall
2) systems that proved their performance in forward-testing
3) systems that are less likely to be correlated (since the futures are 16, and the more systems you trade on those same futures, the more you increase your chance of correlation)

So, all in all, our estimates were not off - even according to my blender the drawdown that happened was very unlikely. The problem is that... we picked too many systems, which inevitably forced them to be:
1) less performing,
2) less forward-tested,
3) more correlated.

If the systems are correlated, the losses happen together, and all your drawdown estimates, shortfall estimates, what have you... they're all off. And the more systems you trade on a fixed number of futures, the more they're likely to be correlated.

Therefore the more you think you're diversifying, if you're not doing it right, the more you're actually doing the opposite, because granted, if you spread out equally, then you're actually diversifying. But if you're, let's say, dealing with so many systems that you do not notice that the last 10 you added are correlated because they're all foreign currencies against the dollar, for example, then you're actually trading the dollar, and you might have changed a balanced portfolio with 10 systems and 10% per non-correlated underlying future, with a new portfolio of 50 systems, of which now 30% is all focused on the same type of correlated futures.

So, the lesson that I draw from this is to always stick to 10 to 20 systems, the best I have, in order to carefully monitor their quality in every detail and potential correlation with each other.

Of course now I am only trading 13 because of my low capital. But as capital will increase, I must not make the mistake of adding any system in excess of 20.

The lesson I draw is that it's better to be trading 10 systems that are different and uncorrelated for sure, rather than 40 systems, whose correlation you cannot keep track of anymore.

Better to choose 10 systems that have a proven forward-tested period, than 40 systems that don't. In fact, the really reliable period is not 1) the back-tested in-sample, nor 2) the back-tested out-of-sample, nor 3) the forward-tested sample, but 4) the sample after you have chosen what you trust and have started monitoring the performance of exactly those futures you have selected as "to be traded". Then, that performance is the performance you can rely on. It is the 4th sample period of a long series of tiring sample periods that have to be monitored and that are the outcome of years of work. The life of a system is like the life of a tree, and you can see all those layers in the bark and stuff. You cannot rely on the forward-tested period, because it's too easy to say "the good systems are those that have performed well in forward-testing". You need to first select those good systems and then pretend you're trading them for a while, and that "while" is the portfolio performance you can expect. Some of them will not keep doing as well as they've been doing, just like in a soccer tournament, the top 3 team will not be the same ones a few months later. Yeah, and there must be a name and a formula for this, too, maybe "survivorship bias" or something, but I know neither.

Another lesson I draw is that it's better to choose 10 systems with an overall profit factor of 2 and small losses, than 40 systems whose losses are bigger and profit factor is lower.

Having said all this, I yet have to find a formula for building a portfolio, especially as far as the number of contracts to be enabled.

Actually a step ahead has been made, because now it's clear to me that the size of the loss is the most important thing, because the size of losses is directly proportional to the shortfall estimates.

In fact, if I could split the contracts, even now, all my problems would be solved. Provided they're not correlated, I would add a large number of systems and increase profit without increasing variability.

If I had a large capital I could already do this, but right now I cannot keep things into the right proportions, because I can barely afford a given variability (having a limited capital).

Let's say the kind of thing I can afford is losses of 200 dollars. I'd size the contracts so to have losses of 200 dollars for every system. Then the systems would compensate one another, and I could trade all the good ones.

But with the contracts there are, some systems with 1 contract have losses of 2000, and those i can't afford. Let alone that i can't afford the margin for others.

So, you can only trade a few contracts, and you can only lower your risk to a point, if you want to make any money, because otherwise you just trade the ZN or the mini-euro, and then you have to wait years before building up any capital (with my systems).

So now I do understand the concept, even though I still don't have a perfect formula.

Empirically I can figure things out.

I will run a test with all my kick ass systems, and pretend they can trade just a quarter of a contract, and see if I can get kick ass results, without much variability.

Like, let's set the objective to making 5k per month (in back-tested period), while having a 95% probability of shortfalls within 5k, which is something that I cannot achieve with full contracts.

There, it worked perfectly:



Instead of 3k per month, I am now (hypothetically) making 6k per month, because - if i could split silver, gold, natural gas contracts - i could afford to trade those very good systems I have on them.

Sounds like the efficient frontier thing. With the same kind of variability I'd be able to increase profit. However, sharpe ratio would not measure it because the number of trades also would increase and therefore the average profit per trade would still have the same relationship to the standard deviation. Yet, sharpe ratio wouldn't tell me. Only my profit and my shortfall estimator tell me. Indeed, as I found out a few days ago, sharpe ratio doesn't care how many trades you stick in the sample (except for the stdev vs stdevp difference, which is irrelevant), because with +2 and -1 always have the same standard deviation AND average profit no matter how many times you repeat them. So it cannot tell you the overall profitability of jack****. I just basically flushed it down the ****ing toilet once and for all - let's not even talk about it anymore.

Instead of getting wins of 2k and losses of 1k, I'd be getting wins of 200 and losses of 100, and they'd be just as good as all the other systems, and add diversification.

On top of it, since they trade at different times, I'd just be adding profit, without requiring any extra investment.

Instead, with the size of contracts they have at CME, I have to be happy with a higher absolute variability, which I cannot afford at the moment.

And so, I either don't trade those systems, or I have a high risk blowing out my account.

 

[Yamato]

just before i flushed the sharpe ratio down the toilet...

I might have to take it all back on the sharpe ratio and how i wanted to flush it down the toilet.

Big mistakes here, due to my math illiteracy.

First of all, avedev() is not stdev() nor stdevp().

For some reason, that I'll find out, avedev() is not the same thing and stdev() actually works better.

[written later: i was wrong - there's practically no difference between them, except that standard deviation is more complicated and equivocal]

And sharpe ratio might actualy be superior to profit factor, despite everything I've been saying. And in that case, I'd put it back.

Ok, here it is:
View attachment comparing_profit_factor_with_sharpe_ratio_and_avedev_with_stdevp.xls

It's officially a mess. Actually I was unsatisfied with profit factor because it rated these two systems exactly the same.



And obviously they're not, because i'd prefer the system with the smaller loss.

So I turned to sharpe ratio, but guess what: it actually favors the system that seems worse to me, the one making the same profit but with a bigger loss. Why is this? Because there's one less trade and so on the numerator what counts is that the average profit is higher.

I guess, once again, we could say, like my quote of someone quoting that professor (in a previous post, yesterday), that "risk is one word but not one number".

Whichever way you look at it, you cannot find one satisfactory formula. So risk is one word, but not one number, nor one formula.

And I guess what I blame sharpe and the others for is giving this false impression. The sharpe ratio is so successful and famous that it doesn't deliver what someone would expect. You'd expect it to be one small concise formula that takes care of everything, and yet it doesn't and it is just as flawed and defective and insufficient as the profit factor and other less known risk metrics. It doesn't deliver what it's known for, and that is why it pisses me off so much. It is concise, it looks good, and it deceives you into thinking that it takes everything into account.

I might as well develop my own empirical recipe, and find a way, hopefully a univocal way, of assessing and selecting systems. But the famous "just maximize the portfolio sharpe ratio" is not the formula that will make it happen, unlike everyone seems to claim.

On the other hand, my math skills are so bad, that I will never again say that I am flushing any formula down the toilet, and from now on, I'll be more respectful to all academics.

The quest that I started in September, to find a univocal and optimal way to select my portfolio is turning out to be much more complex than I thought. If I were to invent what I was looking for, I'd probably deserve a nobel prize.

Here it is:
How The Sharpe Ratio Can Oversimplify Risk

Remember, as Harry Kat, professor of risk management and director of the Alternative Investment Research Center at the Cass Business School in London, said, "Risk is one word, but it is not one number."

 

[Yamato]

discretionary trades still haunting me...

I keep on piling one position on top of the other on my TWS. Ever since the discretionary virus got into me two months ago... I can't get rid of it. I can't heal from it. I keep talking about portfolio theory, and at the same time I engage in the worst possible discretionary trades. Scaling up, martingale, doubling-up on losing trades... a total mess. Up to last week I managed to blow 1000 dollars of the money the systems would have made. Today I blew some more by doing some trading on the GBL. Now I still have one QG and one GBL open positions and I can't close it, psychologically. Also because i feel they should be going my way any time now.

I keep saying to myself: this is the last one. I better not add any contracts to these positions. And wait a few days, make the money and get done with this crap for good, because it's making me lose money and it's keeping me from making money with the systems, since it's using up all my margin. And it's making me waste time and stress and eyesight by staying here in front of the screen and monitoring how the positions go.

It would be about time, after all the blenders, montecarlo, shortfall estimators, that I benefited from the knowledge I acquired and stopped tampering with my systems, let alone adding discretionary trades.

I would gain in health and money. It's about time that I go back to full automation, like I was able to do for a whole year and a half with the investors.

Right now I have those two trades open. Let's try to not add any more. They can stay open for weeks and weeks, without any damage, and potentially with great profit. Let's end all discretionary trading after I am done with these two discretionary trades, which have been an ongoing nightmare for over a month now.

Let's not forget this nightmare, which cost me thousands in terms of profit lost. And dozens of screen hours and health and worries. Let's never forget this. Even if this time my discretionary trading didn't blow out my account, it got very close to it.

 

[Yamato]

Saturday Night Live
SNL Transcripts: Peter Boyle: 02/14/76

 

[Yamato]

2012: The first ten years of the euro banknotes and coins - YouTube

 

[Yamato]

Relationship between bond prices and interest rates - YouTube

 

[Yamato]

STDEVP is directly proportional to AVEDEV and so...

It recently became clear to me that I have to focus on the size of the individual losses (given that I am analyzing profitable systems), and so I have to find the metric that measures it best.

Look at these losses. Which ones are better?



Don't worry about the profit of the system, just focus on the losses.

It's better to take losses of 200 twice or just once? Just once. Yet the denominator of the sharpe ratio, the standard deviation (using stdevp instead of stdev because it avoids differences due to the size of the sample), says that taking it twice, along with a lot of other smaller losses, is "better", because it reduces the standard deviation, and this is because besides the fancy and confusing name, the standard deviation is very close to the mere average absolute deviation, which is very related to the average loss, too. Here, too, the average loss is 150 for a system losing 200 twice, and 200 for a system losing 200 only once. You'd be deceived into thinking that the system with the lower average loss is better, while it's not.

So, if you have a bunch of losses, they average out, and so neither sharpe ratio nor standard deviation are better than the profit factor as far as this, too. What I would need is something that counts all the big losses. I need to find a way for this.

I still don't know if the sharpe ratio is totally discarded and if measures just as much as the profit factor, while being more complicated and equivocal, or if it measures losses more accurately than profit factor, in which case I'd have to adopt it again. The question is what is the best single metric for measuring losses?

 

[Yamato]

objection from a reader on profit factor

I just got alerted by a reader regarding a problem with profit factor: it doesn't show drawdown.

What happens if your system loses for a straight year and then makes money for 3 years in a row? The profit factor will say it's great, and that it has (all other things being equal) a profit factor of 3/1 = 3. But such a system would blow out your account.

My answer is: yes, I know that profit factor isn't perfect and that it does not measure maximum drawdown, as it does not care about the order of the trades.

But, first of all, so far I haven't found anything better, including the sharpe ratio, which also does not measure the order of the trades and therefore the maximum drawdown. And between a very complicated and potentially wrong, flawed, equivocal sharpe ratio and a very simple profit factor, I'd rather stick with what's simpler.

Second of all, provided that the system is not correlated to the underlying future it trades, such prolonged drawdown should only be a matter of chance - and it should not happen (in fact it does not happen on my best systems, and I only trade those). Furthermore, I do not want something that measures drawdown, because, once I have established that the system is not correlated to its underlying future, if a system has five straight losses rather than three, this could very well be a matter of chance.

Think of it this way: would you look for a die that has a lower drawdown? And yet if you take two dice and look at their last x rolls, you will find that they have different drawdowns.

Let us make a clear example and compare two systems with same gross profit and gross loss but a different order of the losses. I want to find out if indeed both sharpe ratio and profit factor ignore the drawdown - as I think.

[...]

Ok, perfect:
View attachment pf_sr_vs_drawdown.xls



They're both incapable of measuring drawdown.

 

[Yamato]

fine tuning my search on downside risk...

As I keep reading the paper by Bertsimas - Lauprete - Samarov, I understand better and better, and I am finding wonderful keywords, that on google return wonderful papers, completely focused on the problem of finding metrics to evaluate performance based on the losses:
http://web.mit.edu/~dbertsim/www/pa...risk measure- properties and optimization.pdf

3.1.4. Relation to lower partial moments
The general idea of downside risk measures has been extensively discussed in the
financial economics literature starting with the safety first approach of Roy (1952) and Markowitz’s (1959) discussion of semi-variance. A more general notion of lower partial moment (LPM) as a measure of risk was introduced and analyzed by Bawa (1975, 1978), Fishburn (1977), and Bawa and Lindenberg (1977), see also more recent papers by Harlow and Rao (1999) and Grootveld and Hallerbach (1999). The LPM of order a with the threshold of a portfolio return X =...

And, from one of these searches, I found this wonderful website here, with both simplified concepts (finally) and formulas:
Investment Performance Analysis & Risk Management - Risk Measurement



Investment Performance Analysis & Risk Management - Shortfall Probability

Shortfall Probability
The shortfall probability is the probability of return falling short of a certain threshold return...

p(sf)= N[{rth - avr} / v ]

p(sf)... shortfall probability
rth... threshold return
avr... average return
v... volatility
N[]... Normal distribution

This calculation assumes that returns are normally distributed. Shortfall probabilities can also be calculated based on alternative distributional assumption or by estimating empirical probabilities from time series.

Ok, in other words, all these search terms is what I need to use to find academic papers talking about my problem: assessing the quality of a (profitable) system based on its losses.

They're on a totally different level than me, they talk about things that I don't understand, but we're really thinking about the same things, so even if I understand 20% of what they say, each time I am getting precious insights.

 

[Yamato]

beyond risk & money management: the birth of Loss Management

After all this talking about "risk", it's about time to find out what the **** is the difference between risk and money management:
Difference between money management and risk management?

Ok, this sucks. I won't even quote it. He's got a gift for complication.

Risk Management

Risk Management Definition | Investopedia

The process of identification, analysis and either acceptance or mitigation of uncertainty in investment decision-making. Essentially, risk management occurs anytime an investor or fund manager analyzes and attempts to quantify the potential for losses in an investment and then takes the appropriate action (or inaction) given their investment objectives and risk tolerance.

Risk management - Wikipedia, the free encyclopedia

As applied to corporate finance, risk management is the technique for measuring, monitoring and controlling the financial or operational risk on a firm's balance sheet. See value at risk.

The Basel II framework breaks risks into market risk (price risk), credit risk and operational risk and also specifies methods for calculating capital requirements for each of these components.

Money Management

Money Management Definition | Investopedia

The process of budgeting, saving, investing, spending or otherwise in overseeing the cash usage of an individual or group.

Money management - Wikipedia, the free encyclopedia

Money management is used in Investment management and deals with the question of how much risk a decision maker should take in situations where uncertainty is present. More precisely what percentage or what part of the decision maker's wealth should be put into risk in order to maximize the decision maker's utility function.

Me thinking

I still can't figure it out. I need to think about it out loud.

Ok, I know what risk is. After all the posts I've talked about it. For a profitable system (and I only use those) "risk" means "potential temporary losses". It doesn't mean "risk of blowing out"... hmm, no, it also means "risk of blowing out". No, wait: it means "risk of blowing out due to potential temporary losses".

So, "risk management" should mean "managing the risk of blowing out due to potential temporary losses".

Ah ah.

So, how do I manage, or better, how do I try to avoid , or better, how do I minimize the risk of blowing out due to potential temporary losses?

Yeah, that's the question. But it can be rephrased in many ways, such as: how do i handle the variability of returns? How do i maximize my profit while minimizing the probability of losing my capital? How do I find the right balance between the probability of increasing my capital and losing it all?

Ok, this is clear. It's not about your edge, but about how much to invest in your edge.

It's not even that. I went too far.

Let's go back to what i wrote earlier: risk management to me is minimizing the risk of blowing out due to potential temporary losses.

So, what is money management?

It bothers me because I achieve risk management by allocating my money, so money management is a tool to manage risk. In fact it is the only tool.

So, can we say that money management is how you manage risk?

Yes, we can.

Fat management is comparable maybe to risk management. We manage our fat by food management, as we manage our risk by managing our money.

So, talking about about risk and money management is equivalent to talking about Fat and Food management. They're synonyms almost, but since managing food intake is the only method of managing fat (forget about managing fat through exercise, for simplicity), then it's faster and more intelligent to call it simply "food management". And certainly we shouldn't talk about both things as if they were two separate entities, like Tom & Jerry.

So, can I say "money management" instead of calling it "risk management"? Or should I say "risk management" instead of calling it "money management"? Not both for sure.

I will call it "risk management", just to remind myself that the real problem for me is blowing out my account. Like someone who wants to eat might want to remind himself that there's a risk of getting fat, if he eats too much.

I want to make money, but I have to be aware of the risks involved in the process. And, obviously, "risk management" is achieved by "money management".

[...]

But you know what? I'd say **** risk management, and take this equivocal term out of our ****ing goddamn mind and dictionary. We don't even know what the **** it means anymore, this goddamn term.

Let's call it "loss management". Losses happen, and therefore we must manage our losses. To minimize the risk of blowing out.

So **** money management and **** risk management. Let's just call it "loss management" from now on.

 

[Yamato]

my baby don't care - YouTube

 

[Yamato]

LeAnn Rimes - Bridge Over Troubled Waters - YouTube

 

[Yamato]

I closed the GBL trade, and I closed a trade on NG, which I had started just two hours earlier (the QG trade is still open). And I missed out on 800 dollars of profit (only made 300). Yeah, after waiting on bund and natural gas, waiting for them to go my way for over a month, when they finally do it, I close the trades early. Happy with just one third of the profit I could have made, today alone.

Why? Not because I didn't want to make more money - there's nothing like self-sabotage like many say - but because I was afraid of losing the profit I had made. Because, after waiting for so many days, and seeing so much red day after day, I could not believe I was being profitable, and I was afraid this profit would be taken away from me. So, that's why I decided to close the trades "while they were profitable".

I overestimated my risk, underestimated my opportunities... due to getting hurt recently.

That's why automated trading is so good - it doesn't get affected by the previous trade, neither in an optimistic way, nor in a pessimistic way. It just assesses its probabilities objectively.

The problem is that my automated systems are so basic (I cannot program everything that's on my mind, I cannot program every opportunity I see - I'd need 1000 systems), that they cannot catch the opportunities I see.

So I try to compensate with discretionary trading, but then... I don't have the ability to manage my positions with the same alertness and patience and every other quality that automated trading has. I enter too early, I add to a losing position, I exit too early... even if the idea was good, I handle it, in the long run, unprofitably. I do not have the capital nor the mind of a discretionary trader. And I don't have the capital, precisely because I do not have the mind, since the capital got destroyed by my actions.

New York, New York (Theme song, 1977) - YouTube

A reader told me, why don't I separate the two accounts? So I could monitor how well I am doing at both. Capital, again. I don't have enough capital to have two separate accounts.

He's right though. This can't go on. I gotta get into movies again. I gotta call the former neighbour and ask her to take me to the movies. Forget about "loss management" for a while. Forget about math. Forget about natural gas. Forget about gbl.

People forget, ignore, that this song is from a movie, and it was written for a movie, and they don't even know that Scorsese directed the movie:
Theme from New York, New York - Wikipedia, the free encyclopedia

"Theme from New York, New York" (or "New York, New York") is the theme song from the Martin Scorsese film New York, New York (1977), composed by John Kander, with lyrics by Fred Ebb. It was written for and performed in the film by Liza Minnelli.

They probably think it's a song for Frank Sinatra, or even by Frank Sinatra.

 

[Yamato]

Simon & Garfunkel - Scarborough Fair - YouTube

 

[Yamato]

I am so pissed off to have missed 400 dollars on GBL and 800 dollars on NG by exiting early. What are you gonna do? If I stayed and looked any longer, I would have placed some revenge trades, and lost maybe 1000 dollars. Yeah because I don't have just the problem of doubling up on losing trades, but also the problem of revenge trades on missed profit. I basically always find a way to constantly hammer myself in the balls. But once again it's not related to subconscious self-sabotage. It's just due to human nature and the counter-intuitive nature of trading. And I don't have the personality required to fix these problems - too proud and impatient. Too used to having my way to adapt to other people and to the market. I keep trying to bend the market to my will. Too self-centered and proud to not take losses personally. So why do I talk about this? Why don't I just stop doing it and forget about it? As I've said, I've got a craving for profit. And I've got nothing to do, and there's huge opportunities in the market - only I can't take advantage of them, because of my personality. It sucks, I suck, **** this. It's so frustrating. I've gotta do stuff. Go to the movies... I've gotta get out.

I've been between 9k and 10k forever. The systems keep making money, and I keep on blowing it. Let alone for the fact that on several instances I've risked blowing out my account due to opening as many contracts as I could afford, and it's a small miracle that I still haven't blown out my account. So, big risk, big stress, big waste of time, and no profit. Loss of sleep... loss of health. ****.

****. I need friends. Good ones. What are friends? I don't even believe in the concept of "friend". To me a human being is something to be avoided, even before knowing him. I just take for granted that people suck, and you have to surprise me by proving me wrong.