Wow, I made it. I got home, and without getting mugged. This time it took me over an hour: some walking, visiting my buddies at Circo Massimo, some bus, some walking again. Each time I get on public transportation it's like gambling with my life. Friday when I was buying tickets at the machine, this guy came up to me and asked me to give him one of the two tickets ("do me a favor: give me one of your tickets" - yeah, he had been observing me in the process of buying the tickets), repeatedly. I felt like asking him if I was being mugged or not: if you're mugging me let me know, and I'll give you what you want. I did not give him any tickets, because I had already been coherced into being generous a few years ago, in the same exact situation, so i was prepared and I replied "I need it...". The good news is that today I didn't get mugged.
No trades open, but everything is working fine as far as automation.
Chopin Nocturne Op. 62 #2 - Rock version - YouTube
[...]
While I'm at it, let's calculate the probability of getting no trades on any given day, and no trades on any given week.
4300 trades across 250 days per year on 2002 to early 2010 = 521 trades per year, but divided by... 250 times 8.25 = 2.1 trades per day. And 4300 trades per 2063 days. Now, how do I calculate the probability in a theoretical way, rather than an empirical one (simply checking the weeks and day when there were no trades)? Do I know how to do this? Can I figure it out?
Let's start simple. If I have 2 weeks, and 2 trades (from a variety of systems), what are my random chances of having those two trades in any given week, any given day, and so on?
There would be a 50% chance of having the first trade on the first week, and 50% of having it on the second week. The same would apply to the second trade. So I think I can safely say that there's 25% of having both trades on week 1 and 25% of having both on week 2. There's 50% that I'll have one trade per week (in either order).
If I had 3 trades, it would be 0.5*0.5*0.5=12.5% of having all of them on any given week... I am already getting lost. I am trying to apply what I studied to a practical purpose, and maybe even to find a practical purpose for what I've studied.
First I should find out the possible outcomes and then I'll worry about the probability.
I don't really need this, but I am trying to use what I studied... it could be useful, a little bit.
Here's something:
Permutations - Free Math Video by Brightstorm
Ok, let's say that each of the 4300 trades could happen in any of the 2063 days (simplified hypothesis, because it is impossible that a system trades twice on the same day).
Oh, ok, it is getting clearer. The chance of a given trade happening on a given day is 1 in 2063. The chance of all trades happening on the same day is 1 in 2063^4300.
The chance of "at least".
With 2 trades in 2 weeks, the chance of at least one trade on a given week is 25% of first trade only, 25% of second trade only, and 25% of both trades. So, at least one trade is 75% and probability can be summed.
And at least one trade on a given day? 10% of first trade only, 10% of second trade only... wait, it's called the
fundamental counting principle:
Fundamental Counting Principal - Free Math Video by Brightstorm
This is how I find the number of different combinations. I have 2 trades that can fall in either of 2 weeks, so it's 2 times 2. So, if I have 3 trades that can happen in 2 weeks, the combinations... should be 3 times 2 = 6? Let's check with the tree diagram.
Wrong. The combinations are 8. And the good ones, with at least 1 trade are 7/8. So in this case it's 2*2*2=8. So I get the number of possible combinations/outcomes by raising the possibilities for each trade to the power of... number of trades. So, if each of 4300 trades can fall in any one of 2063 days, the possible outcomes are 2063^4300. This is a crazy number. But I need to focus on how likely it is to get no trades on a given day and week (i can derive that from the first one), from a theoretical point of view and not an empirical one.
Ok, to get the likelihood of getting no trades on a week, with a total of 3 trades in 2 weeks, I raise the probability of getting no trades to the power of the number of trades:
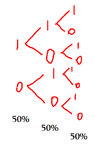
And I get 12.5% probability of getting no trades. I sense that I could derive this number I want from using just a weekly average rather than the total number, but I'll verify later if it's the same thing.
So, what is the probability of not getting trade #1 on a given day? 2062/2063. So if I calculate (2062^4300)/(2063^4300), I should get the probability of not getting any trades on a given day.
Ok, excel goes crazy with these exponents. So I am going to verify if using a weekly average is just as good.
First I'll test it where I can test it to be true.
Ok, let's say I have 21 days and 42 trades (which is also close to being a simplified ratio of my numbers).
There's 20 chances out of 21 that each of the 42 trades will not happen on a given day. That's like 95%... oh ok... how stupid... got it. I don't have to raise to the exponent before doing the division, but I can do it afterwards. This simplifies things a whole lot.
0.95^42=0.13 so my probability of not getting trades on a given day is 13%, with that situation.
Now let's use the previous numbers, and divide the 2062 chances of not getting a trade by the 2063 outcomes. The result is 99.95%. Raise that to 4300. I get 12% probability of getting no trades on a given day.
Let me check this with different numbers to see if it makes sense.
Ok, it works. But now let's see if I could have come up with this in a different way.
Ok, I had the back-tested trades and I had the calendar days of the back-tested period.
I could have come up with an average trade per day, which is 4300/2063 = roughly 2 trades per day. But hey, this doesn't tell me in any way the probability of not getting any trades.
How about 4 trades in 2 days? Could I calculate it in the same way? Now, each of the 4 trades would have a 50% chance of happening on a given day (of the two days). That would mean 0.5 of not happening on a given day, so 0.5^4=0.0625 is the probability of no trades, but this doesn't match my result above, so it would mean that with a shorter sample, I get different results?
I got tired. I wish I didn't have to work all day long. I can't figure it out right now, but I am confident that the 12% is correct.
Let's keep going with that value.
So, if I have a 12% probability of no trades on a given day, what is the probability on a given week? It should be that value raised to the fifth power, which is... 0.002%.
Mmh... let me see if I got any weeks without trades from backtesting. I should have none (except during holidays like christmas). There's almost 500 weeks, so there should be no weeks traded, according to the odds. Let me see...
Perfect: except for christmas/new year (occasionally), there's no weeks without trades. Ok, let's check for days without trades, and keep comparing what statistics say with probability theory predictions.
Oh... what a moron. There is no need for probability based on trades and traded days, because by doing this comparison i was reminded that there's another way to find out... no no, it's different. I just thought that if you see the traded days vs the total number of days, you find out the probability of there being no traded days, but this is empirical, and therefore even more reliable (because the trades are not randomly distributed, in their frequency). Mine was more theoretical... but it did have some empirical data... something like that.
Ok, so if the chance is 12% of having a day without trades, I should find a 12% of days without trades, should I not? It will be interesting to check.
There it is and with this I am done: 1821 traded days on 2063 days. The non-traded days are 242/2063=12%. 12% of estimated probability and 12% of actual statistics. It's unbelievable (not the same exact number, so it's just two similar numbers that I got through different methods). So this proves that you can guess the final statistics from probability theory and viceversa.
Verano Porteño - Astor Piazzolla - Tango - YouTube