You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
- Status
- Not open for further replies.
I can't tell you this. It's a personal question.
Ah ok. I just thought it would read better if we knew her name rather than you having to keep putting "the daughter".
How many dinners did they cost you?
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Yeah, i understand. That makes sense. But I'd rather keep my complaints about people without listing their names. That way I can complain endlessly.
Just one dinner. But right now I can only afford one dinner per month.
Actually I can afford zero dinners per month.
Just one dinner. But right now I can only afford one dinner per month.
Actually I can afford zero dinners per month.
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Candy (2006)
Good anti-conformist movie with heath ledger about heroin:
Candy (2006) - IMDb
Watch Candy online - download Candy - on 1Channel
C.avi | PutLocker
Interesting reading on the subject:
HOW TO QUIT HEROIN COLD TURKEY
Should I quit heroin cold turkey or taper? - Yahoo! Answers
After this experience, after being from a good family, he still died from drug abuse:
Heath Ledger - Wikipedia, the free encyclopedia
Speaking of Ledger. He was going out with the daughter of a trader:
Michelle Williams (actress) - Wikipedia, the free encyclopedia
Candy.Sugar man - YouTube
Sixto Diaz Rodriguez - Wikipedia, the free encyclopedia
The singer who came back from the dead | Music | The Guardian
This director has got to be good, for directing this movie:
http://www.1channel.ch/?&director=Neil Armfield
Damn. There are no more movies by him.
Who knows, maybe he died because he had to practice with drugs to work on this movie.
Too bad I understood very little of the script and I can't find an online script. And the whole forum is still aligned to the left on internet explorer. It has to be fixed.
Good anti-conformist movie with heath ledger about heroin:
Candy (2006) - IMDb
Watch Candy online - download Candy - on 1Channel
C.avi | PutLocker
Interesting reading on the subject:
HOW TO QUIT HEROIN COLD TURKEY
Should I quit heroin cold turkey or taper? - Yahoo! Answers
After this experience, after being from a good family, he still died from drug abuse:
Heath Ledger - Wikipedia, the free encyclopedia
Speaking of Ledger. He was going out with the daughter of a trader:
Michelle Williams (actress) - Wikipedia, the free encyclopedia
Candy.Sugar man - YouTube
Sixto Diaz Rodriguez - Wikipedia, the free encyclopedia
The singer who came back from the dead | Music | The Guardian
This director has got to be good, for directing this movie:
http://www.1channel.ch/?&director=Neil Armfield
Damn. There are no more movies by him.
Sugarman
Won't ya hurry
Coz I'm tired of these scenes
For a blue coin
Won't ya bring back
All those colours to my dreams
Silver majik ships, you carry
Jumpers, coke, sweet MaryJane
Sugarman
Met a false friend
On a lonely, dusty road
Lost my heart
When I found it
It had turned to dead, black coal
Silver majik ships, you carry
Jumpers, coke, sweet MaryJane
Sugarman
You're the answer
That makes my questions disappear
Who knows, maybe he died because he had to practice with drugs to work on this movie.
Too bad I understood very little of the script and I can't find an online script. And the whole forum is still aligned to the left on internet explorer. It has to be fixed.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Solving Literal Equations
I am here now:
Solving Literal Equations - Free Math Video by Brightstorm
This is really great. Simplification is the key to explaining and understanding, and these guys apply the principle really well.
They first stripped it down to all essential concepts, and then they covered them as concisely and simply as possible.
The result is a pleasant course of a few hundred one-minute mini-lessons, that enable you to understand math without going needlessly crazy over it. They do everything quickly and pleasantly. One step after another, they teach you everything you need.
If you sucked at math during junior highschool and highschool, this web site will cure you.
Sixto Rodriguez - Sugar man - YouTube
I realized thanks to these weeks of study that people have problems in math not because they're not intelligent enough but because they're missing knowledge (math terms/concepts).
The difference between math and the other languages is that if you miss a word in English you can still understand the rest, but if you miss a term in math, you can't, and it further prevents you from understanding the other terms.
It's like a big puzzle where you cannot miss one piece. Whereas in a "natural language" you can miss terms and still understand. So it's not about understanding but about knowing, which actually is the same exact thing, and this realization would pretty much make us divide the world between those who know and those who don't know, rather than between stupid and intelligent. But then I'd sum it up by saying that being intelligent means being good at learning, willing to learn, and being good at remembering and categorizing knowledge, and using it (retrieving it from your brain).
So i'd further sum it up by saying that "intelligent" defines someone who is relatively good at acquiring and using knowledge.
Let's see the dictionary:
http://dictionary.reference.com/browse/intelligence
Anyway, I was studying this thing about languages and found a good distinction between natural and artificial languages, starting at this line:
Language - Wikipedia, the free encyclopedia
So math is an artificial language, and english is a natural language.
What's so good about the brightstorm.com guys is that they teach me all the terms i need in a concise and simplified way, which is very effective for me.
I am here now:
Solving Literal Equations - Free Math Video by Brightstorm
This is really great. Simplification is the key to explaining and understanding, and these guys apply the principle really well.
They first stripped it down to all essential concepts, and then they covered them as concisely and simply as possible.
The result is a pleasant course of a few hundred one-minute mini-lessons, that enable you to understand math without going needlessly crazy over it. They do everything quickly and pleasantly. One step after another, they teach you everything you need.
If you sucked at math during junior highschool and highschool, this web site will cure you.
Sixto Rodriguez - Sugar man - YouTube
I realized thanks to these weeks of study that people have problems in math not because they're not intelligent enough but because they're missing knowledge (math terms/concepts).
The difference between math and the other languages is that if you miss a word in English you can still understand the rest, but if you miss a term in math, you can't, and it further prevents you from understanding the other terms.
It's like a big puzzle where you cannot miss one piece. Whereas in a "natural language" you can miss terms and still understand. So it's not about understanding but about knowing, which actually is the same exact thing, and this realization would pretty much make us divide the world between those who know and those who don't know, rather than between stupid and intelligent. But then I'd sum it up by saying that being intelligent means being good at learning, willing to learn, and being good at remembering and categorizing knowledge, and using it (retrieving it from your brain).
So i'd further sum it up by saying that "intelligent" defines someone who is relatively good at acquiring and using knowledge.
Let's see the dictionary:
http://dictionary.reference.com/browse/intelligence
Pretty close. Actually mine is better.capacity for learning, reasoning, understanding, and similar forms of mental activity; aptitude in grasping truths, relationships, facts, meanings, etc.
Anyway, I was studying this thing about languages and found a good distinction between natural and artificial languages, starting at this line:
Language - Wikipedia, the free encyclopedia
Human languages are usually referred to as natural languages, and the science of studying them falls under the purview of linguistics. A common progression for natural languages is that they are considered to be first spoken and then written, and then an understanding and explanation of their grammar is attempted.
An artificial language is a language the phonology, grammar, and/or vocabulary of which have been consciously devised or modified by an individual or group, instead of having evolved naturally.
So math is an artificial language, and english is a natural language.
What's so good about the brightstorm.com guys is that they teach me all the terms i need in a concise and simplified way, which is very effective for me.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Math in HTML
Now I am working here again:
Math - Algebra
Amazingly, there is a method in html to write the exponent other than "^":
–4x2+47x–112 = –2x2+27x–70
But I still haven't figured out how to do it. Furthermore when the post got published the appearance changed.
Got it:
Math in HTML (and CSS) - presenting mathematical expressions on Web pages
Damn. It got published wrong again.
Here's the html code:
I'll try writing it like this:
[SUP CLASS=exponent]2[/SUP]
Now like this:
[SUP]2[/SUP]
No, it doesn't work.
I give up. This forum interface doesn't take that code. I'll keep using "^".
Now I am working here again:
Math - Algebra
Amazingly, there is a method in html to write the exponent other than "^":
–4x2+47x–112 = –2x2+27x–70
But I still haven't figured out how to do it. Furthermore when the post got published the appearance changed.
Got it:
Math in HTML (and CSS) - presenting mathematical expressions on Web pages
The HTML language has the sub and sup elements for subscripts and superscripts. But they should primarily be regarded as stylistic suggestions only, rather than as essential parts of the notation. (See my notes on the intended use of sub and sup.) Naturally they can be valuable for “styling” math, too. To quote the descriptions of sub and sup in WDG’s HTML 4.0 Reference, replacing their markup examples with their appearance on your browser:Since SUB is inherently presentational, it should not be relied upon to express a given meaning. However, it can be useful for chemical formulas and mathematical indices, where the subscript presentation is helpful but not required. For example:
- Chemical formulas include H2O (water) and C21H27NO (methadone).
- Let x = x1 + x2 + ... + xn.
Since SUP is inherently presentational, it should not be relied upon to express a given meaning. However, it can be useful for mathematical exponents where the context implies the meaning of the exponent, as well as other cases where superscript presentation is helpful but not required. For example:However, especially when superscripting is used to express exponentiation, superscripting is essential, and there need not be any contextual hints. It really makes a difference if 109, which is intended to mean 10 to the power 9, actually gets displayed as 109. The same applies to using superscripts e.g. in denoting the transpose of A by AT (i.e., A immediately followed by T in superscript style).
- The rent is due on the 1st of each month.
- An example of a quadratic polynomial is 3x2 + 5x - 7.
Damn. It got published wrong again.
Here's the html code:
<SUP CLASS=exponent>2</SUP>
I'll try writing it like this:
[SUP CLASS=exponent]2[/SUP]
Now like this:
[SUP]2[/SUP]
No, it doesn't work.
I give up. This forum interface doesn't take that code. I'll keep using "^".
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
subtraction by regrouping
Ingenious!
Subtraction by Regrouping (Borrowing)
Who would have ever thought I'd have spent time on a web site for children, but believe it or not, after using excel for 20 years, I don't know how to do things they teach you in elementary school.
This is one ingenious way, when you have neither excel nor can you afford to do things in your head due to the number being big.
I came across this problem and had to solve it, because I was doing the long division, which requires you to know the subtraction:
Long Division
And I was doing the long division, because I was doing these exercises (roots):
Math - exponent
As I said before, in math one thing calls another, and if you want to do things right, you cannot afford to skip anything. So for me this meant and will mean going back to elementary school.
All in all, long division is a really cool invention if you think about it...

And if you think about it, i bet there's a lot of college educated people who don't know how to do it anymore:
Long division - Wikipedia, the free encyclopedia
Cool. Thanks to math, I get to be in 5th grade again.
Now I need to ace these things, these "things" being... the algorithms/procedures for the "basic operations of arithmetic":
Everyday Mathematics (Chicago Math) Basic Algorithms
Elementary arithmetic - Wikipedia, the free encyclopedia
How many people know the things taught at the link above? A minority. Excel and modern technology unteach everything.
Like the programmer I met on skype, who told me that my question "what is -2^2" was "fairly basic stuff" and then proceeded to tell me the wrong answer of "4", and then spent the next half an hour trying to talk his way out of it, and further insulting me ("it depends on how it's written" and "only newbies have problems with this", etc.).
Elementary arithmetic instead rules, and that's where all your math problems begin, and that's where you have to go back if you want to solve them. But the problem is that excel and technology unteach everything, even if you were lucky enough to have good teachers in elementary school.
But before getting started on arithmetic, I need to study something even more fascinating, the history of arithmetic:
Arithmetic - Wikipedia, the free encyclopedia
There's probably people who gave their life to invent the long division.
You see, for us it all begins here, in elementary school:
Addition
But for mankind, this is the end result of thousands of years of work by mathematicians. It is the "method of the Indians", as Fibonacci said in his Liber Abaci. He went to school in North Africa, where he learned it, and brought it to Europe.
Tonight, when I'll get home, I'll resume studying math from here:
Addition
You see, we are taught in elementary school mathematical knowledge that took thousands of years to be accumulated. No wonder it doesn't stick. We're taught math as if it were something natural and implicit in nature, but this is bull****. Math was invented by humans and it took thousands of years to find an effective way of doing it, and it could have gone the other way. The decimal system is not the only way things can be. Instead we're taught as if everything had been there since the beginning of time. So what I am saying is that history should be the first subject. History of math, history of all the languages we're taught, history of science, history of everything. For example, geography. 500 years ago we didn't even know that the earth was a ball. We should be told that as well, along with all the bull**** notions forced into our minds. History would help us like the subjects. There should be more reasoning and less memorization. A different attitude. If it just meant showing a movie on the history of each subject, it should be done.
Ingenious!
Subtraction by Regrouping (Borrowing)
Who would have ever thought I'd have spent time on a web site for children, but believe it or not, after using excel for 20 years, I don't know how to do things they teach you in elementary school.
This is one ingenious way, when you have neither excel nor can you afford to do things in your head due to the number being big.
I came across this problem and had to solve it, because I was doing the long division, which requires you to know the subtraction:
Long Division
And I was doing the long division, because I was doing these exercises (roots):
Math - exponent
As I said before, in math one thing calls another, and if you want to do things right, you cannot afford to skip anything. So for me this meant and will mean going back to elementary school.
All in all, long division is a really cool invention if you think about it...

And if you think about it, i bet there's a lot of college educated people who don't know how to do it anymore:
Long division - Wikipedia, the free encyclopedia
Today, inexpensive calculators and computers have become the most common way to solve division problems, decreasing the traditional educational imperative to know how to do so by paper and pencil techniques. (Internally, those devices use one of a variety of division algorithms). In the United States, long division has been especially targeted for de-emphasis, or even elimination from the school curriculum, by reform mathematics, though traditionally introduced in the 4th or 5th grades. Some curricula such as Everyday Mathematics teach non-standard methods, or in the case of TERC argue that long division notation is itself no longer in mathematics. However many in the mathematics community have argued that standard arithmetic methods such as long division should continue to be taught.[2]
Cool. Thanks to math, I get to be in 5th grade again.
Now I need to ace these things, these "things" being... the algorithms/procedures for the "basic operations of arithmetic":
Everyday Mathematics (Chicago Math) Basic Algorithms
Elementary arithmetic - Wikipedia, the free encyclopedia
How many people know the things taught at the link above? A minority. Excel and modern technology unteach everything.
Like the programmer I met on skype, who told me that my question "what is -2^2" was "fairly basic stuff" and then proceeded to tell me the wrong answer of "4", and then spent the next half an hour trying to talk his way out of it, and further insulting me ("it depends on how it's written" and "only newbies have problems with this", etc.).
Elementary arithmetic instead rules, and that's where all your math problems begin, and that's where you have to go back if you want to solve them. But the problem is that excel and technology unteach everything, even if you were lucky enough to have good teachers in elementary school.
But before getting started on arithmetic, I need to study something even more fascinating, the history of arithmetic:
Arithmetic - Wikipedia, the free encyclopedia
There's probably people who gave their life to invent the long division.
The prehistory of arithmetic is limited to a small number of artifacts which may indicate conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC although its interpretation is disputed.[2]
The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but the characteristics of the particular numeral system strongly influence the complexity of the methods. The hieroglyphic system for Egyptian numerals, like the later Roman numerals, descended from tally marks used for counting. In both cases, this origin resulted in values that used a decimal base but did not include positional notation. Although addition was generally straightforward, multiplication in Roman arithmetic required the assistance of a counting board to obtain the results.
Early number systems that included positional notation were not decimal, including the sexagesimal (base 60) system for Babylonian numerals and the vigesimal(base 20) system that defined Maya numerals. Because of this place-value concept, the ability to reuse the same digits for different values contributed to simpler and more efficient methods of calculation.
The continuous historical development of modern arithmetic starts with the Hellenistic civilization of ancient Greece, although it originated much later than the Babylonian and Egyptian examples. Prior to the works of Euclid around 300 BC, Greek studies in mathematics overlapped with philosophical and mystical beliefs. For example, Nicomachus summarized the viewpoint of the earlier Pythagorean approach to numbers, and their relationships to each other, in his Introduction to Arithmetic.
Greek numerals, derived from the hieratic Egyptian system, also lacked positional notation, and therefore imposed the same complexity on the basic operations of arithmetic. For example, the ancient mathematician Archimedes devoted his entire work The Sand Reckoner merely to devising a notation for a certain large integer.
The gradual development of Hindu-Arabic numerals independently devised the place-value concept and positional notation, which combined the simpler methods for computations with a decimal base and the use of a digit representing zero. This allowed the system to consistently represent both large and small integers. This approach eventually replaced all other systems. In the early 6th century AD, the Indian mathematician Aryabhata incorporated an existing version of this system in his work, and experimented with different notations. In the 7th century, Brahmagupta established the use of zero as a separate number and determined the results for multiplication, division, addition and subtraction of zero and all other numbers, except for the result of division by zero. His contemporary, the Syriac bishop Severus Sebokht described the excellence of this system as "...valuable methods of calculation which surpass description". The Arabs also learned this new method and called it hesab.
Although the Codex Vigilanus described an early form of Arabic numerals (omitting zero) by 976 AD, Fibonacci was primarily responsible for spreading their use throughout Europe after the publication of his book Liber Abaci in 1202. He considered the significance of this "new" representation of numbers, which he styled the "Method of the Indians" (Latin Modus Indorum), so fundamental that all related mathematical foundations, including the results of Pythagoras and the algorism describing the methods for performing actual calculations, were "almost a mistake" in comparison.
In the Middle Ages, arithmetic was one of the seven liberal arts taught in universities.
The flourishing of algebra in the medieval Islamic world and in Renaissance Europe was an outgrowth of the enormous simplification of computation through decimal notation.
You see, for us it all begins here, in elementary school:
Addition
Addition is ...
... bringing two or more numbers (or things) together to make a new total.
[...]
Example: If you add 2 and 3 you get 5. You would write it like this:
2 + 3 = 5
But for mankind, this is the end result of thousands of years of work by mathematicians. It is the "method of the Indians", as Fibonacci said in his Liber Abaci. He went to school in North Africa, where he learned it, and brought it to Europe.
Tonight, when I'll get home, I'll resume studying math from here:
Addition
You see, we are taught in elementary school mathematical knowledge that took thousands of years to be accumulated. No wonder it doesn't stick. We're taught math as if it were something natural and implicit in nature, but this is bull****. Math was invented by humans and it took thousands of years to find an effective way of doing it, and it could have gone the other way. The decimal system is not the only way things can be. Instead we're taught as if everything had been there since the beginning of time. So what I am saying is that history should be the first subject. History of math, history of all the languages we're taught, history of science, history of everything. For example, geography. 500 years ago we didn't even know that the earth was a ball. We should be told that as well, along with all the bull**** notions forced into our minds. History would help us like the subjects. There should be more reasoning and less memorization. A different attitude. If it just meant showing a movie on the history of each subject, it should be done.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Re: doing it all over again, from pre-algebra
Getting back to this post i wrote a while ago (cfr. above and link below):
http://www.trade2win.com/boards/trading-journals/85510-my-journal-2-a-325.html#post1702448
I do not understand why dewey classifies arithmetic after algebra. It's not in alphabetical order, so what order is he following. I would have thought that arithmetic came before algebra, not just as far as teaching but also as far as when it was invented.
From:
List of Dewey Decimal classes - Wikipedia, the free encyclopedia
510 Mathematics
You know what? I'll just do it all over again, why not.
I am starting from pre-algebra. I like this web site and it will be pleasant:
Algebra - Math - Brightstorm
Besides, now I know the history of maths, so I am comfortable with studying these things, given that for every little video I watch, there's one guy who gave his life to work out the formulas and notation used in it.
Yeah, I guess this recipe for learning could be applied to any subject: a little bit of history, a little bit of theory and a little bit of practice. When you start out, you need a reason to learn it: so you need practice first, to show you that you need math, which is what happened in my case with losing money in the stock market due to a lack of portfolio theory. Then, once you realize you need theory, it is still not enough, because there's a whole lot of theory to cover, and you will give up if you do it all at once. So you need to approach it a little bit at a time, and need some history. Then you go back to theory. Then some practice. Then history, and so on. If you ever get lost into theory just go back to history, videos... backwards to simpler stuff. You can't learn math all at once, just like i didn't learn english all at once.
Like for English, the problem with math is not about being intelligent enough to understand formulas, but about being knowledgeable enough to know the mathematical notation. The problem with all of us is that we think we're not understanding because we're stupid, and then this makes us give up. Instead it is just like any other language, and it takes more learning than reasoning.
AREAS OF MATHS
In my effort to cover maths, but only the maths that I need, I will try to define a structure of a few branches of maths, or areas, so i can cover it correctly and not randomly and disorderly. I want to be as orderly as possible:
Areas of mathematics - Wikipedia, the free encyclopedia
Way too many on wikipedia's entry above.
This one's interesting, too, but too many once again:
Outline of mathematics - Wikipedia, the free encyclopedia
I will use this guy:
Melvil Dewey - Wikipedia, the free encyclopedia
List of Dewey Decimal classes - Wikipedia, the free encyclopedia
Screw Topology. I will never need it.
[...]
Done. TIring but absolutely worth it.
View attachment 123686
Now, with this healthy and orderly structure (not too many categories nor too few), I am ready to immerse myself into math and learn to swim in it.
Getting back to this post i wrote a while ago (cfr. above and link below):
http://www.trade2win.com/boards/trading-journals/85510-my-journal-2-a-325.html#post1702448
I do not understand why dewey classifies arithmetic after algebra. It's not in alphabetical order, so what order is he following. I would have thought that arithmetic came before algebra, not just as far as teaching but also as far as when it was invented.
From:
List of Dewey Decimal classes - Wikipedia, the free encyclopedia
510 Mathematics
- 511 General principles
- 512 Algebra & number theory
- 513 Arithmetic
- 514 Topology
- 515 Analysis
- 516 Geometry
- 517 Not assigned or no longer used
- 518 Numerical analysis
- 519 Probabilities & applied mathematics
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
algorithms/procedures for the 4 basic operations of arithmetic
Finally.
I managed to gather all the mathematical knowledge up to the times of Fibonacci, and where did I find it? At the beginning of mathsisfun.com, which is an area of the web site meant for children below 10 years old.
Here is the four precious procedures that I forgot along the years (by using computers and calculators):
Addition in Columns
Subtraction by Regrouping (Borrowing)
Long Multiplication
Long Division to Decimal Places
Things like these are forgotten because it's almost as if these manual methods were inferior to calculators, whereas they're in fact superior, or rather they make a person superior, because he can then do things without the need of a calculator/computer.
I need to ace these procedures.
By the way, I just checked if one can say "mathematical knowledge" and in fact it is redundant in a way, in an historical sense, and in a linguistic sense, because...
Mathematics - Wikipedia, the free encyclopedia
So, if we cared about the meaning of words, "mathematical knowledge" would be as meaningless as saying "knowledge of knowledge".
[...]
Great start. I practiced and practiced and i just totally aced the "addition in columns" procedure:
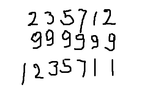
If i had a child with me during these few days, I could make him skip a 5 grades within a few weeks of teaching him. Instead of sitting in a class bored for 5 years, he'd then move on to college, directly. No need for 10 years of bull****, boredom and so on.
[...]
Wow.
Subtraction is even more fascinating.
Subtraction by Regrouping (Borrowing)
But one must not get confused... and mix these procedures with one another.
On the other hand, they all have in common one thing: it's all about the decimal system and positional notation:
Positional notation - Wikipedia, the free encyclopedia
Queen Lily Of The Valley - YouTube
Done with "subtraction by regrouping" as well. I did their "super hard worksheet" and got everything right:

Tomorrow I'll focus on long division (to decimal places) and long multiplication.
[...]
Here it is, the thing i was talking about:
How do I teach subtraction with regrouping of zeros? - Yahoo! Answers
Children often end up disliking math because first of all they don't know why they are learning math, and second of all they don't understand why things happen the way they happen. They should be taught history of math, and positional notation as opposed to Roman Numerals and Egyptian numerals. You know what i am saying? Things would be much clearer and interesting.
Instead they're rushed into this memorization process and told "that's just the way it is". You don't know why you're studying it, you don't know why things work that way... it's crap. Everything should begin from history.
They should be told: "people had this need and, to respond to this need, they invented numbers, and different people invented different numbers..." and so on.
[...]
It's interesting how these procedures are given redundant names in order to differentiate them from the corresponding operations (the concept of addition, subtraction, etc.): addition in columns, subtraction by regrouping, long multiplication, and long addition.
Anyway, here's another exercise i did, where in one shot, i combine addition in columns and subtraction by regrouping.
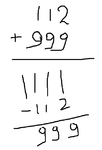
The conquest of math continues.
[...]
Ok. I have done also long multiplication and long division. Now I'll practice while going to work. I am done. I need a lot of practice now. I will have a calculator in my mind thanks to this method.
And, most importantly, the more i do math, the less I will be scared when faced with the final task: portfolio theory.
Finally.
I managed to gather all the mathematical knowledge up to the times of Fibonacci, and where did I find it? At the beginning of mathsisfun.com, which is an area of the web site meant for children below 10 years old.
Here is the four precious procedures that I forgot along the years (by using computers and calculators):
Addition in Columns
Subtraction by Regrouping (Borrowing)
Long Multiplication
Long Division to Decimal Places
Things like these are forgotten because it's almost as if these manual methods were inferior to calculators, whereas they're in fact superior, or rather they make a person superior, because he can then do things without the need of a calculator/computer.
I need to ace these procedures.
By the way, I just checked if one can say "mathematical knowledge" and in fact it is redundant in a way, in an historical sense, and in a linguistic sense, because...
Mathematics - Wikipedia, the free encyclopedia
Mathematics (from Greek μάθημα máthēma "knowledge, study, learning") is the study of...
So, if we cared about the meaning of words, "mathematical knowledge" would be as meaningless as saying "knowledge of knowledge".
[...]
Great start. I practiced and practiced and i just totally aced the "addition in columns" procedure:
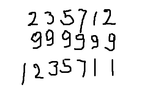
If i had a child with me during these few days, I could make him skip a 5 grades within a few weeks of teaching him. Instead of sitting in a class bored for 5 years, he'd then move on to college, directly. No need for 10 years of bull****, boredom and so on.
[...]
Wow.
Subtraction is even more fascinating.
Subtraction by Regrouping (Borrowing)
But one must not get confused... and mix these procedures with one another.
On the other hand, they all have in common one thing: it's all about the decimal system and positional notation:
Positional notation - Wikipedia, the free encyclopedia
Positional notation or place-value notation is a method of representing or encoding numbers. Positional notation is distinguished from other notations (such as Roman numerals) for its use of the same symbol for the different orders of magnitude (for example, the "ones place", "tens place", "hundreds place"). This greatly simplified arithmetic and led to the quick spread of the notation across the world.
Queen Lily Of The Valley - YouTube
Done with "subtraction by regrouping" as well. I did their "super hard worksheet" and got everything right:

Tomorrow I'll focus on long division (to decimal places) and long multiplication.
[...]
Here it is, the thing i was talking about:
How do I teach subtraction with regrouping of zeros? - Yahoo! Answers
My little brother came up to me and asked for help in his math homework. His problem is $100.00 - 55.99 the answer is 44.01 but he wanted to explain why. How can I explain regrouping with multiple zeros' to him instead of just saying, " That's the way it is?" My little brother is in third grade.
Children often end up disliking math because first of all they don't know why they are learning math, and second of all they don't understand why things happen the way they happen. They should be taught history of math, and positional notation as opposed to Roman Numerals and Egyptian numerals. You know what i am saying? Things would be much clearer and interesting.
Instead they're rushed into this memorization process and told "that's just the way it is". You don't know why you're studying it, you don't know why things work that way... it's crap. Everything should begin from history.
They should be told: "people had this need and, to respond to this need, they invented numbers, and different people invented different numbers..." and so on.
[...]
It's interesting how these procedures are given redundant names in order to differentiate them from the corresponding operations (the concept of addition, subtraction, etc.): addition in columns, subtraction by regrouping, long multiplication, and long addition.
Anyway, here's another exercise i did, where in one shot, i combine addition in columns and subtraction by regrouping.
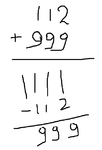
The conquest of math continues.
[...]
Ok. I have done also long multiplication and long division. Now I'll practice while going to work. I am done. I need a lot of practice now. I will have a calculator in my mind thanks to this method.
And, most importantly, the more i do math, the less I will be scared when faced with the final task: portfolio theory.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
moving on... to summation notation exercises
Ok, I am done with the procedures for the four basic operations of arithmetic, and, even though I'll keep practicing them on the way home in the taxi for the next several days, I will soon have to move on to some different exercises, those on summation notation, for which I will need a computer.
Indeed I recently finished reading this long but very well written manual on summation notation:
http://www.statpower.net/Content/310/Summation Algebra.pdf
Now, while it's fresh, I need to find out if I know and have understood everything. So next I need to find exercises for summation notation.
Then I will resume my work on equations, on brightstorm.com.
Then, once i will be done with arithmetic and algebra, I will be able to move on to probability theory, within statistics, which is within the branch of applied mathematics.
And then, finally, I will be able to read any article/book on portfolio theory.
[...]
Ok, here are the best links for summation notation exercises:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
http://www.maths.mq.edu.au/numeracy/web_mums/module4/Worksheet46/module4.pdf
http://mash.dept.shef.ac.uk/Resources/sigma.pdf
Summation Notation by columbia.edu
Summation Notation by jwbales.us
http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/summationdirectory/Summation.html
Pretty good to see that I am finally at a college level, and not preschool anymore.
[...]
Ok, done with this:
Summation Notation by columbia.edu
It was clear and simple. I've gone through worse concepts when reading the manual here:
http://www.statpower.net/Content/310/Summation Algebra.pdf
Ok, I've done this, too:
Summation Notation by jwbales.us
And practiced some concepts I hadn't fully realized.
Now I have 4 more web sites to go:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
http://www.maths.mq.edu.au/numeracy/web_mums/module4/Worksheet46/module4.pdf
http://mash.dept.shef.ac.uk/Resources/sigma.pdf
http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/summationdirectory/Summation.html
[...]
Ok, I have done this, too:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
Only 3 more to go: one australian, one british, one american.
Ok, now I got as far as example 5 of page 2 of the australian web site. I have to stop because I have to go to sleep.
Ok, I am done with the procedures for the four basic operations of arithmetic, and, even though I'll keep practicing them on the way home in the taxi for the next several days, I will soon have to move on to some different exercises, those on summation notation, for which I will need a computer.
Indeed I recently finished reading this long but very well written manual on summation notation:
http://www.statpower.net/Content/310/Summation Algebra.pdf
Now, while it's fresh, I need to find out if I know and have understood everything. So next I need to find exercises for summation notation.
Then I will resume my work on equations, on brightstorm.com.
Then, once i will be done with arithmetic and algebra, I will be able to move on to probability theory, within statistics, which is within the branch of applied mathematics.
And then, finally, I will be able to read any article/book on portfolio theory.
[...]
Ok, here are the best links for summation notation exercises:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
http://www.maths.mq.edu.au/numeracy/web_mums/module4/Worksheet46/module4.pdf
http://mash.dept.shef.ac.uk/Resources/sigma.pdf
Summation Notation by columbia.edu
Summation Notation by jwbales.us
http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/summationdirectory/Summation.html
Pretty good to see that I am finally at a college level, and not preschool anymore.
[...]
Ok, done with this:
Summation Notation by columbia.edu
It was clear and simple. I've gone through worse concepts when reading the manual here:
http://www.statpower.net/Content/310/Summation Algebra.pdf
Ok, I've done this, too:
Summation Notation by jwbales.us
And practiced some concepts I hadn't fully realized.
Now I have 4 more web sites to go:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
http://www.maths.mq.edu.au/numeracy/web_mums/module4/Worksheet46/module4.pdf
http://mash.dept.shef.ac.uk/Resources/sigma.pdf
http://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/summationdirectory/Summation.html
[...]
Ok, I have done this, too:
http://www.mathcentre.ac.uk/resources/leaflets/firstaidkits/2_22.pdf
Only 3 more to go: one australian, one british, one american.
Ok, now I got as far as example 5 of page 2 of the australian web site. I have to stop because I have to go to sleep.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
back at the office
Back at work.
In the cab I practiced the algorithms for the four arithmetic operations.
Today I have a sore throat.
The colleague in my room, I never complained about him, but he's now starting to annoy me. He jokes around too much and I cannot focus on my work. He's also rude, because when he comes back, if I am on the phone, he should not say hi, loudly as he does, and make me look like I am working at the fish market instead of an office. I wish this guy just disappeared, like most of the other roommates I had. On the other hand, he is not the worst roommate I ever had, and the room is a great room otherwise, far away from the other colleagues. But when he's not here it's much better.
Now I need to brush my teeth.
I have 2 more hours to go.
I have to finish a job for another office. They keep lending me out to other offices to do excel work. I am ok with learning things, because I feel I am needed. The only problem is that my roommate keeps on talking to me endlessly, and I can't be as efficient as I'd like to be. Talking is a big waste of time.
Now he went to lunch, so I can finally rest and stop smiling at his stupid jokes.
He's quite competent but he doesn't work much. Long coffee break in the morning, lots of phone calls not related to work but for his own private matters, long lunch break of over one hour, and on top of all this, he comes to work one hour late. And on top of this, he spends another two hours wasting my time with his jokes. He probably works 4 hours per day, at the most.
But he's really proud of himself and how diligent and conscientious he is.
He rarely works, but despite that, he works more than the average colleague. He works only half of the time, but for those 4 hours, he works well. The average colleague works only 4 hours, and works badly.
Me, I work 100% of the time and do my best. But no one appreciates it, or rather no one rewards it, so I started doing my own work. Even now I am working for example. I never stop working.
Now I will brush my teeth, and then I'll do that thing for that guy from the other office. Then the stats. And then I'll go home and resume my summation notation exercises. But if I get tired of them, as I am expecting, for today I will switch to some brightstorm.com videos on equations. What matters is keeping my interest alive. Boredom is what kills your learning. Your attention drowns in boredom, so you should never push yourself so hard as to be bored. Which instead is what happens in school: in every subject they push you so hard and focus so much on theory that you quickly fall into a deep state of boredom, and start resenting the subjects, the teachers and your learning is then compromised.
Learning is like a fire that is fueled by knowledge rather than wood, and that begins with something sparking your attention. You answer that question, but then you have another question, and the fire keeps burning and building up: question, answer, question, answer... If they feed you answers without you first raising the questions, it's like putting too much wood into a fire, suffocating it. The forcing knowledge into your head done by teachers is like forcing wood into a fire at a rate faster than it can burn. You put the fire out, and put your attention out, and halt learning.
So basically I started the fire by watching the marcus du sautoy "story of maths" series, and now I am try to keep it burning. But I can't go too fast or too slowly in feeding it wood, and I have to feed the right type of wood. As I move along the fire (my understanding) will get bigger and it will burn almost any type of wood, but right now I still have to be careful and neither exaggerate nor run out of things to burn.
Back at work.
In the cab I practiced the algorithms for the four arithmetic operations.
Today I have a sore throat.
The colleague in my room, I never complained about him, but he's now starting to annoy me. He jokes around too much and I cannot focus on my work. He's also rude, because when he comes back, if I am on the phone, he should not say hi, loudly as he does, and make me look like I am working at the fish market instead of an office. I wish this guy just disappeared, like most of the other roommates I had. On the other hand, he is not the worst roommate I ever had, and the room is a great room otherwise, far away from the other colleagues. But when he's not here it's much better.
Now I need to brush my teeth.
I have 2 more hours to go.
I have to finish a job for another office. They keep lending me out to other offices to do excel work. I am ok with learning things, because I feel I am needed. The only problem is that my roommate keeps on talking to me endlessly, and I can't be as efficient as I'd like to be. Talking is a big waste of time.
Now he went to lunch, so I can finally rest and stop smiling at his stupid jokes.
He's quite competent but he doesn't work much. Long coffee break in the morning, lots of phone calls not related to work but for his own private matters, long lunch break of over one hour, and on top of all this, he comes to work one hour late. And on top of this, he spends another two hours wasting my time with his jokes. He probably works 4 hours per day, at the most.
But he's really proud of himself and how diligent and conscientious he is.
He rarely works, but despite that, he works more than the average colleague. He works only half of the time, but for those 4 hours, he works well. The average colleague works only 4 hours, and works badly.
Me, I work 100% of the time and do my best. But no one appreciates it, or rather no one rewards it, so I started doing my own work. Even now I am working for example. I never stop working.
Now I will brush my teeth, and then I'll do that thing for that guy from the other office. Then the stats. And then I'll go home and resume my summation notation exercises. But if I get tired of them, as I am expecting, for today I will switch to some brightstorm.com videos on equations. What matters is keeping my interest alive. Boredom is what kills your learning. Your attention drowns in boredom, so you should never push yourself so hard as to be bored. Which instead is what happens in school: in every subject they push you so hard and focus so much on theory that you quickly fall into a deep state of boredom, and start resenting the subjects, the teachers and your learning is then compromised.
Learning is like a fire that is fueled by knowledge rather than wood, and that begins with something sparking your attention. You answer that question, but then you have another question, and the fire keeps burning and building up: question, answer, question, answer... If they feed you answers without you first raising the questions, it's like putting too much wood into a fire, suffocating it. The forcing knowledge into your head done by teachers is like forcing wood into a fire at a rate faster than it can burn. You put the fire out, and put your attention out, and halt learning.
So basically I started the fire by watching the marcus du sautoy "story of maths" series, and now I am try to keep it burning. But I can't go too fast or too slowly in feeding it wood, and I have to feed the right type of wood. As I move along the fire (my understanding) will get bigger and it will burn almost any type of wood, but right now I still have to be careful and neither exaggerate nor run out of things to burn.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Some more progress, and some bigger pieces of wood are now burning in my intellectual fire:
Solving Literal Equations - Free Math Video by Brightstorm
The fire is still burning well, even though I've already run out of paper and alcohol ("the story of maths"), so now I need to keep feeding the fire bigger pieces of wood, which I have to find on the web, or the fire will run out of fuel and it will go out.
If instead I tried to feed markowitz's formulas to the fire, it would go out immediately. I am still unable to process them, and my understanding would be overwhelmed.
Solving Literal Equations - Free Math Video by Brightstorm
The fire is still burning well, even though I've already run out of paper and alcohol ("the story of maths"), so now I need to keep feeding the fire bigger pieces of wood, which I have to find on the web, or the fire will run out of fuel and it will go out.
If instead I tried to feed markowitz's formulas to the fire, it would go out immediately. I am still unable to process them, and my understanding would be overwhelmed.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
it's all over
Du Sautoy and his Story of Maths documentary have really made me aware of death and there's no undoing that. Ever since watching that documentary I've been thinking about death. Everything has been relativized as a consequence. The investors stealing my systems, the Nobel Prize I won't win for economics. The assholes I banned on this journal. We're just names on a history book. We're history. Right now I am at a point in Maslow's hierarchy of needs where I won't be forgetting death for a while. It doesn't matter if I sleep, it doesn't matter if I succeed, nothing matters. I might study math as a pastime. And just in case I fall lower in Maslow's hierarchy and need to make money to survive. Actually even going to work is going to be a pastime. It's going to make everything effortless. Especially human relationships. Everything is now looking very small. People are looking small, almost invisible.
Du Sautoy and his Story of Maths documentary have really made me aware of death and there's no undoing that. Ever since watching that documentary I've been thinking about death. Everything has been relativized as a consequence. The investors stealing my systems, the Nobel Prize I won't win for economics. The assholes I banned on this journal. We're just names on a history book. We're history. Right now I am at a point in Maslow's hierarchy of needs where I won't be forgetting death for a while. It doesn't matter if I sleep, it doesn't matter if I succeed, nothing matters. I might study math as a pastime. And just in case I fall lower in Maslow's hierarchy and need to make money to survive. Actually even going to work is going to be a pastime. It's going to make everything effortless. Especially human relationships. Everything is now looking very small. People are looking small, almost invisible.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Obviously this thinking about death didn't make me any more relaxed, because it's not a relaxing thought. In fact, many things I said were not exact, and many worries will stay in my mind.
For example, I can't sleep and might have to go to work late tomorrow, and whereas I should not care, because going to work should be irrelevant, instead I still feel guilty.
And I am still pissed that the forum is aligned to the left.
And I am still pissed about many other things.
Anyway, I don't have to write a treatise on anything.
I'm gonna watch some more brightstorm.com videos.
I love this lady:
http://www.brightstorm.com/math/algebra/solving-equations/percent-change/
Getting tougher. Now the lessons last 6 minutes instead of 2:
http://www.brightstorm.com/math/alg...-inequalities/introduction-to-absolute-value/
For example, I can't sleep and might have to go to work late tomorrow, and whereas I should not care, because going to work should be irrelevant, instead I still feel guilty.
And I am still pissed that the forum is aligned to the left.
And I am still pissed about many other things.
Anyway, I don't have to write a treatise on anything.
I'm gonna watch some more brightstorm.com videos.
I love this lady:
http://www.brightstorm.com/math/algebra/solving-equations/percent-change/
Getting tougher. Now the lessons last 6 minutes instead of 2:
http://www.brightstorm.com/math/alg...-inequalities/introduction-to-absolute-value/
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Doing a little better. I am destined for greatness. Maybe it's a delusion that took over after thinking about death for a few weeks, or maybe it's real and it's the truth, as it now seems to me. Either way right now I am thinking that I am destined for greatness and that I am unstoppable.
Today I didn't go to work, because, given that I am destined for greatness, I can afford to spit on my job. And they accepted it, given that they know how great I am. I didn't exactly text message them "i am destined for greatness and today I will not come" but rather "I am sick and I am not coming today", but that's just because I am so modest. The truth is that I think I am too good for them, and they know it is the truth. That's why I got away with so much in all these years. If it's a delusion, it is a collective one, shared by all those around me.
Today I will take it easy. I will watch some movies, I will sleep. And, when bored, I will do some math. I have ordered all my math wood to burn in the intellectual fire I have started a few weeks ago. The wood is ordered in 5 groups, and i will feed it to the fire, depending on the type of flame and needs of the moment:
For every folder I have a "what_was_the_last_subject_I_covered" subfolder, which tells me how far I got last time. I just found something new and amazing about my hypersnap software (the only software I ever paid for): it has an Optical Character Recognition function. If you take a snapshot of black text on white background, it automatically converts it into text:
HyperSnap has achieved greatness, and using great programs will further enhance my greatness. I am a demigod. And since I believe in myself, I am not atheist anymore. I am now a demi-believer.
"Don't Speak" live on OMGuitar (iPad) - YouTube
Today I didn't go to work, because, given that I am destined for greatness, I can afford to spit on my job. And they accepted it, given that they know how great I am. I didn't exactly text message them "i am destined for greatness and today I will not come" but rather "I am sick and I am not coming today", but that's just because I am so modest. The truth is that I think I am too good for them, and they know it is the truth. That's why I got away with so much in all these years. If it's a delusion, it is a collective one, shared by all those around me.
Today I will take it easy. I will watch some movies, I will sleep. And, when bored, I will do some math. I have ordered all my math wood to burn in the intellectual fire I have started a few weeks ago. The wood is ordered in 5 groups, and i will feed it to the fire, depending on the type of flame and needs of the moment:
01_brightstorm.com
02_summation_notation
03_thatquiz.org
04_math-tests.com
05_equation_generator-solver
For every folder I have a "what_was_the_last_subject_I_covered" subfolder, which tells me how far I got last time. I just found something new and amazing about my hypersnap software (the only software I ever paid for): it has an Optical Character Recognition function. If you take a snapshot of black text on white background, it automatically converts it into text:
What is TextSnap™
TextSnap™ technology included in HyperSnap 6 allows you to capture editable text from many places on the screen, where regular text copy/paste functions are not available. It is not intended to replace copy/paste for text editors (like MS Word, email programs, HTML authoring tools etc.) but rather to quickly snap text from program dialog boxes, menus, error messages that pop up on the screen, list of files from folder windows etc. Of course, from many editors TextSnap™ will capture text as well.
Limitations of TextSnap™
Here are the limitations, as we determined them so far: TextSnap™ will NOT capture text from:
Adobe Acrobat and Acrobat Reader (PDF files). This is normally not a big problem, just choose selection tool from Acrobat Reader toolbar, or right-click text and select "Allow Hand Tool to Select Text", and you may use normal copy/paste there.
Programs written in Java, running in Java virtual machine.
Text that is embedded on bitmap images (JPEG, PNG, GIF, TIFF, BMP etc.)
HyperSnap has achieved greatness, and using great programs will further enhance my greatness. I am a demigod. And since I believe in myself, I am not atheist anymore. I am now a demi-believer.
"Don't Speak" live on OMGuitar (iPad) - YouTube
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
I bet this is going to be good:
Watch Sahara online - download Sahara - on 1Channel
[...]
No, I was wrong. Something wrong with the recipe. Some ingredients were quite good. Probably the plot was bad.
Watch Sahara online - download Sahara - on 1Channel
[...]
No, I was wrong. Something wrong with the recipe. Some ingredients were quite good. Probably the plot was bad.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
I need to reorganize my plan and resources
So far I have had several fronts, each with its own characteristics:
1) the youtube/wikipedia history of math research:
I am finished with this phase. It was easy, pleasant, but limited. Watching a nice video on the history of math is not going to make me learn math. It will make me curious about math, make me stop disliking it, but it will not teach me enough about math.
2) the portfolio theory books:
This is exactly the final objective of all this work I am doing, but I am not ready for that, and if I face markowitz's articles and books right now, I get stopped at the second page of every one of them. I think if I should resume this phase on textbooks easier than markowitz's.
3) the brightstorm.com videos:
I should keep doing this until I have finished watched all their (100s of) videos. This is clear, pleasant, and I learn how to do math, but keeping things at this level can only get me so far because I cannot just memorize pages and pages of formulas, without using them for anything.
NEW PLAN
I have successfully gotten rid of my fear for formulas. I have successfully resumed my studying, as if I still were in highschool. Which is an achievement.
Now I need to accompany my study of formulas with portfolio theory textbooks. With a practical use of the notation/concepts I am studying, I will have new questions and enhance the scope of my studying.
I must not lose sight of the point of all this, or my attention will weaken.
So. What books should I start with?
I cannot do markowitz, and I cannot do wikipedia which is way too hard. Check this out:
http://en.wikipedia.org/wiki/Modern_portfolio_theory#Mathematical_model
I ain't ready for it yet.
So I am going to need to find articles on portfolio theory that give me a taste of formulas, but do not overwhelm me with them.
At any rate, if anything goes wrong and I do not proceed according to this plan, I just have to make sure that the math fire keeps burning and I keep going forward, regardless of what I'll be doing. Even if this means just watching brightstorm.com videos endlessly. Even if it means focusing on just equations and without any practical use for them. I cannot afford to stop for a period longer than 24 hours, or there's a risk that I'll never resume. Let's not forget that I am still paying up my butt for renting a server in the US, and that my investments are on hold because of my portfolio theory ignorance. I am not on hold for any other reason. Yes, I don't have any money to invest right now, but if I had it, I wouldn't be ready to invest it. I need to first find the recipe for making the systems work together in an efficient and automated way.
So. Speaking of simplified articles on portfolio theory, this is the stuff I need to be reading:
http://www.riskglossary.com/link/portfolio_theory.htm
I need to find another 200 of these links, get acquainted with the concepts and formulas they use, provided they're not as dense as markowitz's nor as those you find on wikipedia.
Now I can take a break. The only rule I'll have is that I cannot stop doing math for longer than 24 hours. It has to become like brushing my teeth. I need to conquer math and formulas.
So far I have had several fronts, each with its own characteristics:
1) the youtube/wikipedia history of math research:
I am finished with this phase. It was easy, pleasant, but limited. Watching a nice video on the history of math is not going to make me learn math. It will make me curious about math, make me stop disliking it, but it will not teach me enough about math.
2) the portfolio theory books:
This is exactly the final objective of all this work I am doing, but I am not ready for that, and if I face markowitz's articles and books right now, I get stopped at the second page of every one of them. I think if I should resume this phase on textbooks easier than markowitz's.
3) the brightstorm.com videos:
I should keep doing this until I have finished watched all their (100s of) videos. This is clear, pleasant, and I learn how to do math, but keeping things at this level can only get me so far because I cannot just memorize pages and pages of formulas, without using them for anything.
NEW PLAN
I have successfully gotten rid of my fear for formulas. I have successfully resumed my studying, as if I still were in highschool. Which is an achievement.
Now I need to accompany my study of formulas with portfolio theory textbooks. With a practical use of the notation/concepts I am studying, I will have new questions and enhance the scope of my studying.
I must not lose sight of the point of all this, or my attention will weaken.
So. What books should I start with?
I cannot do markowitz, and I cannot do wikipedia which is way too hard. Check this out:
http://en.wikipedia.org/wiki/Modern_portfolio_theory#Mathematical_model
I ain't ready for it yet.
So I am going to need to find articles on portfolio theory that give me a taste of formulas, but do not overwhelm me with them.
At any rate, if anything goes wrong and I do not proceed according to this plan, I just have to make sure that the math fire keeps burning and I keep going forward, regardless of what I'll be doing. Even if this means just watching brightstorm.com videos endlessly. Even if it means focusing on just equations and without any practical use for them. I cannot afford to stop for a period longer than 24 hours, or there's a risk that I'll never resume. Let's not forget that I am still paying up my butt for renting a server in the US, and that my investments are on hold because of my portfolio theory ignorance. I am not on hold for any other reason. Yes, I don't have any money to invest right now, but if I had it, I wouldn't be ready to invest it. I need to first find the recipe for making the systems work together in an efficient and automated way.
So. Speaking of simplified articles on portfolio theory, this is the stuff I need to be reading:
http://www.riskglossary.com/link/portfolio_theory.htm
I need to find another 200 of these links, get acquainted with the concepts and formulas they use, provided they're not as dense as markowitz's nor as those you find on wikipedia.
Now I can take a break. The only rule I'll have is that I cannot stop doing math for longer than 24 hours. It has to become like brushing my teeth. I need to conquer math and formulas.
Last edited:
Yamato
Legendary member
- Messages
- 9,840
- Likes
- 246
Moving forward but need to speed up:
Solving Multi Step Inequalities - Free Math Video by Brightstorm
My attention is weakening. I need to speed up or I'll be ****ed. There's a risk of losing momentum.
It's a mined field. New field. I am ignorant. Danger of getting lost.
Solving Multi Step Inequalities - Free Math Video by Brightstorm
My attention is weakening. I need to speed up or I'll be ****ed. There's a risk of losing momentum.
It's a mined field. New field. I am ignorant. Danger of getting lost.
- Status
- Not open for further replies.
Similar threads
- Replies
- 10
- Views
- 3K
- Locked
- Replies
- 27
- Views
- 7K