interesting puzzle on squaring a negative number
Did you know that the exponent gets calculated before the sign?
Order of operations - Wikipedia, the free encyclopedia
But then excel does it differently, and just about everyone has his own opinion on it. Wikipedia has one:
Plus and minus signs - Wikipedia, the free encyclopedia
Order of operations - Wikipedia, the free encyclopedia
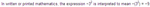
As they say in wikipedia (cfr.picture above), minus three to the second is equal to minus nine. Always. And this is because of the ("PEMDAS") order of operations. First you calculate the exponent and you get 9, and then you use the operator, which makes it become negative.
But then Yahoo answers has another:
The square number of negative number is ......? - Yahoo! Answers India
It is tough indeed. And it's not "irrelevant" as someone just told me on skype. It's a major issue.
Google has another answer:
minus two to the second - Google Search
Excel behaves differently, too:

Does it make any sense that 0-2^2 is different from -2^2 ? Yet that is the way it is for excel. Much like the guy i met on skype said, if the number is all by itself, it is considered one way, and if it is near another number it is considered another way.
Wikipedia does not agree with it, nor does google.
Please no one post any superficial opinions on this or I will ban you as usual. I did a lot of research and I can't stand it if someone shows up and writes his superficial opinion as if it were a fact.
[...]
Here's another one in contrast with Yahoo Answers and Excel:
Squares and Square Roots

I don't wanna hear any moron telling me that this is trivial. If we can't reach a univocal answer on this, we cannot go any further. We can't just say like i heard from someone on skype "you just use the parentheses and eliminate the doubt". I want to know what i do when i find it without parentheses, NOT what i have to to do to be clear.
And so far one guy says one thing and another guy says another. Yesterday my dad ask his physicist friend what is "minus two squared", and he answered "four". I still believe this is wrong, and I want to get to the bottom of this. And given that all math books tell me i am right and "minus two squared is minus four" and that all the conceited people in the world instead tell me "of course minus two squared is four", I want to prove them wrong.
Then what makes me angry is they try to talk their asses out of it by accusing me of being ignorant or implying i don't know math or by saying "things are only sometimes ambiguous when you don't have a full understanding". Damn moron. This guy went from saying that it was unequivocal to saying it was equivocal because I am ignorant to saying it was equivocal because "math is language" and has limits, to saying that "pedantically" i was right, and stayed as conceited as he was at the start. If you were wrong then admit it. I cannot accept being treated as an idiot from someone who's actually wrong about what he's saying.
[...]
Here it is, finally. Dr. Math agrees with me, and disagrees with the conceited and ignorant science people of the world:
Math Forum - Ask Dr. Math
Question:
Negative Numbers Combined with Exponentials
Date: 03/09/2001 at 01:07:20
From: Dee Ryno
Subject: Negative numbers combined with exponentials.
I know that -3 ^2 {to the second power} is negative 3 because the
order of operations tells us exponentials are done first and then the
answer {9} is multiplied by (-1), but why isn't the negative attached
to the -3 to say -3 * -3, which would make it positive, since 3 ^2
{to the second power} is 3 * 3? Help.
This has confused a lot of teachers too!
Dee
Answer:
Date: 03/09/2001 at 15:29:24
From: Doctor Peterson
Subject: Re: Negative numbers combined with exponentials.
Hi, Dee.
You are aware that the order of operations is the key. Because
negation is taken as a multiplication, and exponentiation is done
before multiplication, we read
-3^2
as
-(3^2)
rather than as
(-3)^2
The exponent holds on to the 3 tighter than the minus sign does.
I think you're asking why we have this rule, when the minus looks so
close to the 3, and it seems so much more natural to think of it as -3
squared. I could just say this is a choice that has been made, and we
just follow the convention. But there's an additional reason besides
the logic of seeing negation as multiplication by -1. When we get to
algebra and want to write polynomials, we find ourselves working with
-x^n, which has to follow the same rules as for -3^n:
x^3 - 3x^2 - 3x + 5 = 0
There's little question here; we know that 3x^2 is taken as 3(x^2),
and then we subtract that. But what about
-x^3 - 3x^2 - 3x + 5 = 0 ?
Do we take this as (-x)^3 or as -(x^3)? Because this is a polynomial,
we know that x is meant to be the base of all the exponents; we don't
want to have to write -(x^3) to make it mean what we intend; so we are
perfectly happy to follow the logic where it takes us and treat the
negation as a multiplication done after the exponentiation, rather
than as a part of the base. The rule helps here, rather than seeming
odd: In a polynomial we want exponents to come before everything else,
because they are the stars of the show.
I suspect that polynomials drove much of the development of the order
of operations; many of the early examples of algebraic notation in
which those rules can be discerned are polynomials.
- Doctor Peterson, The Math Forum
The Math Forum - Ask Dr. Math
Math is unequivocal. It's you guys who are conceited and ignorant and have the nerve to tell me things like "things are only sometimes ambiguous when you don't have a full understanding". Instead I would change that sentence into "Things are unequivocally wrong and you're so conceited that you won't admit it".
It's unbelievable how far ignorance can go. Even excel is wrong and says that "-2^2" is "4". That's not because they're right. That's because when they made excel, there was an ignorant programmer who coded it this way. Like the programmer I met today and told me I was wrong. So now we know that being a programmer doesn't mean you're good at math.
Here's another bunch of conceited idiots:
Is a -9 to the second power a positive result ? Does anyone know a rule applying to this type of question? - Yahoo! Answers
Here's the beginning of what was voted "best answer":
(-9)^2 is a positive result -- 81.
This is because (-9)^2 = -9 * -9, and the product of two negative numbers is always positive...
Everyone kept saying how the product of two negative numbers is always positive, but this is overshadowing the fact that he did not say (-9), but only -9, and therefore since, as Dr.Math says, "exponentiation is done before multiplication", the result is, once again, -81.
So we have a bunch of people on yahoo answers (and on skype) who are spreading ignorance on the web, and now maybe I will be called ignorant as a consequence, because the rule becomes the wrong version and ignorance rules (just like in the "Idiocracy" movie). But the problem is that there's still a large majority of mathematicians who agree with me. It's only the conceited ignorant people who are spreading ignorance. Now the problem becomes if some of the ignorant crowd become programmers and turn excel into something ignorant. Then people start saying crap like "things are only sometimes ambiguous when you don't have a full understanding", then crap like "math is a language" and so there's "ambiguities", and then "yes, you're pedantically right". When instead they are wrong and won't admit it, and they're spreading ignorance while calling others ignorant.
[...]
Here's another ignorant mother ****er:
What does -4 to the second power equal
Whenever you square a negative number it becomes positive. so -4^2 is -4*-4=16.
Be careful though. (-4)^2 is not the same as -(4^2).
He asked neither of your answers. He asked -4^2 and the answer is -16, but you pretended he asked (-4)^2 and replied 16, which is not the case because that is not what he asked.
[...]
This is someone on my side again:
Positive and negative numbers - This DOESN'T MAKE SENSE!!! - College Confidential
Ok so my book says: -3^2 = -9 and (-3)^2 = 9
When the -3 is in the parentheses it means you are multiplying -3 x -3, equaling 9. Without the parentheses, you are multiplying 3 x 3, and adding the negative to it, equaling -9. With that idea -
-3^2 = -9
[...]
And finally a yahoo answers guy knowing how to ask a (rhetorical) question (by giving himself the answer) so to spread some knowledge on the web:
Negative number to an even power? - Yahoo! Answers
Negative number to an even power?
Why do so many people think that a negative number ie -2 to an even power ie 2 as in -2^2 has an even answer as in
-2^2 = 4
when the correct answer is -4?
Additional Details
edit:
I meant a positive answer not an even answer.
without parenthases -2^2 = -4 is the correct answer
-3^2 = -9
Even in these answers some people are saying the answer is positive or it depends on grouping. If useing parenthases then it does depend on grouping but without the answer is always negative.
Pretty neat. There's so much ignorance that he still got the wrong answers, even after giving the answer himself, and they ended up choosing as best answer, the usual lame answer, "they're both right, depends on how you write it", which is the usual bull**** because he did write it one way and it can only be interpreted in one way, since he did write it.
Here's another one by dr.math, and once again, of course, it agrees with me (this question was asked 4 years before the other one, cfr.quote above):
Math Forum - Ask Dr. Math
Question:
Exponents and Negative numbers
Date: 03/02/97 at 11:15:14
From: Anonymous
Subject: Exponents and negative numbers
Dear Dr. Math,
In different texts about this same question, I can find two different
answers. The solution to: (-3)squared = 9. But when -3 is squared
(without the brackets), one source may say 9 while another source
says -9.
In context, the -3 squared used in sequence will always be -9; why
would the exponent apply to the negative sign unless it is enclosed
by a sign of grouping? In short, why wouldn't the answer to -3
squared, standing alone and without parenthesis or brackets, be -9?
Thanks very much.
Sincerely,
Marvin E. Crim
Answer:
Date: 03/09/97 at 14:53:39
From: Doctor Ken
Subject: Re: exponents and negative numbers
Hi Marvin -
After a lengthy discussion among the Drs. Math to make sure we had our
facts straight, I think we have an answer for you.
If you ever see the expression -3^2 evaluated as 9, that's incorrect.
The exponentiation is always done before the negation unless there are
parentheses there to indicate otherwise.
However, there are some contexts in which it _looks_ like texts are
saying that -3^2 = 9, but a closer inspection will either reveal a
subtle interpretation or a misunderstanding. For instance, what is the
difference between the following statements:
"If I take negative three and square it, I get nine."
"If I square negative three, I get nine."
"If I evaluate negative three squared, I get negative nine."
"If I take the opposite of three squared, I get negative nine."
All of the above statements are correct. The reason some of them
end up with 9 as the answer and some end up with -9 is that some of
the statements have groupings implied in their phrasing. The first
two statements translate into algebraic notation as (-3)^2 = 9, the
third statement translates to -3^2 = -9, and the fourth statement
translates to -(3^2) = -9.
So the confusion here is not really about mathematical notation, it's
about how to translate English into mathematical notation. Either
that, or your textbook is incorrect!
I hope we've cleared up some confusion. The bottom line is that
-a^b is always evaluated as -(a^b).
-Doctor Ken, The Math Forum
Check out our web site!
The Math Forum - Ask Dr. Math
So you heard that. Either that, or there's a mistake. If it is written -2^2 then it is always -4. So excel is wrong, too. And all these conceited mother ****ers are wrong as well. So **** you all for wasting my ****ing time.
This is yet another situation where there's a majority who is wrong (all confused by the rule "Whenever you square a negative number it becomes positive") and a minority who is right.
The textbooks are usually right, but they're written by a minority of people. Instead the web, since the majority gets to write on it, is mostly wrong, and gives you the wrong answer. So the few informed people (like me) are overwhelmed by the ignorant people. But then one wonders: in the dictionary after a while, if everyone says something one way, then the ignorant version takes over and it becomes the rule. Will it be the same for math? I don't think this is as likely. I don't think the widespread ignorance about mathematical notation will change mathematical notation.
[...]
After 4 years of harassment (questions) even Dr.Math is changing his mind. Damn. They harassed him out of his knowledge:
Math Forum - Ask Dr. Math
Squaring Negative Numbers
Date: 02/19/2002 at 10:59:10
From: Thanh Phan
Subject: Squaring negative numbers
Hello,
I would like to know: does -9^2 = 81 or -81?
--------------------------------------------------------------------------------
Date: 02/19/2002 at 12:38:08
From: Doctor Rick
Subject: Re: Squaring negative numbers
Hi, Thanh.
You really should be precise about what you are asking in this case,
since (-9)^2 means -9 times -9, but the expression -9^2 could also be
taken to mean -(9^2), that is, the negative of the square of 9, which
is -81.
When we're working with variables, if we see -x^2, we interpret it in
the second way, as -(x^2), because squaring (or any exponentiation)
takes precedence over negation (or any multiplication; -x is treated
as -1*x.
When you have numbers only, as in -9^2, it's not at all clear that we
should treat it differently from -x^2. However, some will argue that
it should, because -9 represents a single number, not an operation on
a number. Thus, some will interpret -9^2 as (-9)^2, while others will
read it as -(9^2).
Because of the difference of opinion, I highly recommend that you put
in the parentheses explicitly whenever this situation arises.
- Doctor Rick, The Math Forum
The Math Forum - Ask Dr. Math
No no... wait. There's 3 different doctors. It was first Peterson, then Ken and now Rick. So this is even better because 3 different experts gave 2 answers in favor of my version and more in favor than against it (this last one).
Ok, I asked my own Yahoo question, and already got lots of answers:
Why such ignorance about squaring negative numbers, as in "-2^2"? - Yahoo! Answers
This is pretty good and it is raising some doubts in my mind:
You are incorrect in thinking PEDMAS has anything to do with this. If a number is negative, well then it is negative, it isn't a function that you do after parenthesis, exponents, mult/divide.....
If a number is negative, it is on the opposite side of 0 on the number line than it's positive counterpart, so that is a trait of the number, not something you may do to it later.
Judging by your post, I don't think you will believe this, so hopefully thousands of years of mathematicians much smarter than you, doing it the way you think is false, will convince you.
Finally, a big part of your example is if you are squaring negative 2, which would be (-2)^2, or are you taking the negative of 2 squared, which would be -(2^2). Trust me when I say both of these work out as they should, the first is 4 & the second is -4, regardless of your opinion.
This bill guy seems quite authoritative, with his insulting tone, but it's not enough to convince me. He makes something that might be a good point, in his first paragraph, but given all the mathematicians that I read on the web... it seems just his opinion, along with all the ignorant guys, against all the mathematicians.
Besides, I got a whole lot of other yahoo answers agreeing with me.
And I have this authoritative wolfram dude on my side, too:
-2^2 - Wolfram|Alpha
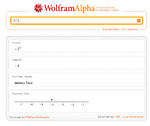
Best answer so far:
Why such ignorance about squaring negative numbers, as in "-2^2"? - Yahoo! Answers
Unary minus is usually given lower precedence than exponentiation, but as you found out this is not always the case. According to Wikipedia, Microsoft Excel and also the programming language bc give unary minus higher precedence
Order of operations - Wikipedia, the free encyclopedia
As someone with hands in both mathematics and programming, I can say Excel and bc are atypical in this regard. For example, in Haskell -2^2 evaluates to -4, and in Perl and Python -2**2 evaluates to -4. In fact, until about a year ago, I didn't know that the convention used in Excel existed.
Different authors/fields use different notations/conventions, it's as simple as that. In general, such differences don't cause significant communication problems except for those who are not familiar with the territory (read: newbies!). It can be an inconvenience, but it's hard to eliminate because the conventions are embedded in the literature/language.
Specialists understand that different conventions exist, and they choose a convention appropriate in their field and communicate accordingly. When in doubt, notation can be defined before it is used.
I disagree with your claim that having different notations makes mathematics inexact. It's analogous to one author writing in English and another in French. Sure, it might cause problems if you can't read French, but that doesn't invalidate anything. And in reality the differences in notation are not nearly as dramatic as the differences between English and French.
I liked this last one and I chose it, even though it is partly wrong. This guy is saying that there's a different spelling and that such spelling is like French. Instead that spelling is nothing more than a widespread "misspelling". Just because one of the many misspellers is none other than Excel, it doesn't make it "French". It is still a misspelling, especially in math. Then he goes on to say that it causes me confusion only because I am a "newbie", and he basically also implies that I am not knowledgeable enough to criticize. But dude, it's precisely the foreigners and the children who pick out the mistakes in a language that is foreign to them and that they are discovering. The others might have gotten used the mistake. So it's precisely the newbies you should rely on to find mistakes in your language. At least as far as the intelligent and precise ones like me, because the others will simply learn what the majority uses, which is the wrong form, and that is how it becomes widespread, and how Idiocracy comes true.
So it's not english vs french but it's correct spelling vs misspelling. And yes, it might become the rule, since that's the way it works with misspellings. And yes, now we're at a point where you call it a different language. Just like American, which became a new language, whereas at the start it was considered just a bunch misspellings. But my question (and it was my question from the start on yahoo answers, cfr. above) was precisely if we will go, even in a precise science like math, towards Idiocracy and its spellings:
Idiocracy Mash-up - YouTube
Idiocracy - Trailer - YouTube
But you see, we cannot afford to have 2 different math spellings, so in this case either British or American will have to prevail. Well, you get my point and you get the situation here. I am learning English, but I am neither in the UK nor in the US, and I am having to choose between two different spellings: the good one, and the wrong one, and I wanted to make the right choice as I don't want to cover all the material with the wrong spelling (US English, which later became an acceptable spelling).
I still can't believe this programmer friend of mine on "skype" (just like many others answering this question on the web) told me it was "fairly basic stuff" treating me like an ignorant or an idiot and then proceeded to give me the wrong answer, which is:
-2^2=4
I can't stand being treated as stupid/ignorant especially if it's not a "minor issue" and by someone who doesn't know the answer.