my journal 3

[Yamato]

more on the "portfolio theory for dummies" concept

I need to break portfolio theory into smaller steps. These books I have on my signature (Chan, Cover, Grinold-Kahn, Thorp, Vince) represent steps too big for me (even Chan, which is the easiest) to be overcome and I am going to end up quitting the endeavor, if I just keep on trying to read them from cover to cover.

There's nothing like Khan Academy for portfolio theory. It's interesting.

Whereas math educators make it easy because they are aiming their work to children (among which retarded adults like me), for portfolio theory it's either no material or it is material for mathematicians and physicists. And so you have a lot of traders who use rule-of-thumb approximate methods, because they're having the same problems I am having. I might do that, too, but I'll try this route a little longer.

I yet have to find a book for me.

Even Chan is too hard for me. His chapter six I mean, the one on portfolio theory.

Since the kelly criterion is the simplest thing, and since everyone talks about it in their portfolio theory books, I am going to keep trying the "kelly criterion for dummies" venue. That's the best I can think of, to break my task into smaller steps.

 

[Yamato]

ok, back with more on the kelly criterion

I know I am going really slow, but this is the only pace I can afford without running out of breath. I guess I am burned out. I used to be more intelligent than this. Too much office has worn me out.

Here's my latest attempt (this time it works):


The rest of the file works as well (the chart is on it, along with the table and the formulas):
View attachment kelly_criterion_20120225.xls

This workbook reflects what this video is talking about (I wish I were this guy):
Understanding Kelly Criterion - YouTube

And, despite having plotted it, I still cannot quite make sense of how you could lose by having such an edge and by betting more than 50% of your capital. As I often say, this is counter-intuitive.

It's going to take a whole month and another 30 videos before i understand all the facets of this counter-intuitive phenomenon.

And even then, of course, it will be just the start of portfolio theory, because kelly doesn't work with futures, unless you have an infinite capital. Indeed, with a capital of 10k, forget about dividing my contracts into smaller contracts. Once I lose a few thousands, I can't keep trading anymore. This is just the start. Let's just try to get started on the right foot.

[...]

You know what? For a while this concept of "feat" and "endeavour" helped me do work, because the exercises were either done or not done, but right now, with these complex portfolio theory subjects, I have to adopt a more relaxed approach, one without daily deadlines. I'll do it as it comes, without any daily targets. I know I have the will to work, but dividing this subject by daily targets has proven to be at this point very counterproductive, especially because there's nothing like the Khan Academy of portfolio theory, so I am going to be frustrated that i don't reach a daily target, but it would not be my fault, since there's no tiny steps pre-organized for me, like at khan's. So from here on, I have the material, I don't know how I'll cover it, but, until i get some portfolio theory material that is doable because it's divided into understandable small steps, forget about a daily target as I've been having for the past 5 months.

 

[Yamato]

expecting vs delivering

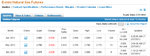
I was expecting this of my systems, when I enabled them six weeks ago: 1167 dollars per week (forward-tested average return).

How did they perform?

As expected, since whoever did best is not always who will do best in the future, they did not perform as well, in the last six weeks: 550 dollars per week.

Yeah, half as much. That is exactly in line with what we saw with the investors. Fascinating. Things change, people change, seasons change, moods change, but the numbers of statistics stay the same.

Paranoid Android (Radiohead) on violin & piano - Entropy Ensemble - YouTube

Of course I am still hoping that they'll do a little better in the future weeks, because I chose them very carefully this time (cfr. previous one thousand posts). Yeah, 'cause this time... I was aware, and méfiant.

Aware : Van Damme s'explique - YouTube

[...]

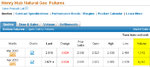
Sharpe ratio was 2.12 in backtesting. In forward-testing it was 2.67 (that's why/how i chose them). In the traded period the sharpe ratio was 1.98. I'd say it is acceptable, despite the fact that the profit was half as much.

Now I'll try to resample the trades, to see what risk exactly I am running of blowing out the account.

The trades were 61. I multiplied them by 1067, so I filled up all the 65k rows. Then I attached to each trade/row the usual excel rand() function and re-ordered them accordingly, thereby resampling them.

Now I will get a correct estimate of how likely I am to blow out, if things keep going as they've been going in real trading (which is more reliable than back-testing, and also more reliable than forward-testing).

I have fallen in love with this resampling methodology I invented, after studying some probability. I don't even remember how I came up with it - i wrote some posts about it.

[...]

Ok, done.

This is really when I can say something with confidence about my systems. Because it's not just the back-testing, not just the out-of-sample test of the back-testing, not just the forward-testing, but it is the real trading. I can at least expect them to behave in the future as they have behaved in real trading - that much I can expect, at least for the short term (that is to say that I am not expecting the same kind of performance three years from now).

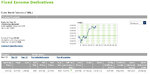
And here's the results.

In back-testing things were like this:

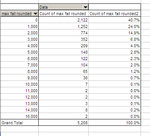
97.6% chance of survival with the present level of capital (roughly 9500 dollars).

In back-testing resampled it was like this, a bit worse:

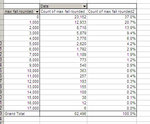
96.1% chance of survival. Pretty close to the regular back-testing.

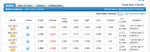
In forward-testing of course it was better, because I chose the systems I chose, precisely because of their performance. But this is forward-testing resampled so it's a bit worse:

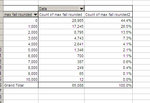
99.5% chance of survival. But this, despite being forward-tested is the trickiest one, because I chose the systems that worked best, so of course their performance is excellent - or else I would not have chosen them.

And finally, here's what really counts - the six weeks of real trades (a total of 61 trades) resampled:

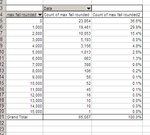
Damn! 99.5% chance of survival again. And there's no error. This reminds me a lot of the normal distribution, the way my drawdowns are distributed.

Anyway, despite the fact that the money made was less than what forward-tested would have made me expect, the losses were just as small as in the forward-tested period. I mean, combined together, my chance was the same. And this is quite likely to stand the test of time.

While I am at it, I will calculate the normal distribution thing... just to refresh my memory on what I've studied.

Ok, let me think... mumble mumble... what do I do first. I calculate the standard deviation of all the drawdowns. That's going to take a while.

Moron! I don't have to do it manually. Excel has a function. I will use stdevp(). It makes no difference anyway, on 65 thousand cases.

Ok, the rule was that 68% of cases should be within 1 standard deviation. 95% within 2, 99.7% within 3. Did I remember right?

68-95-99.7 rule - Wikipedia, the free encyclopedia



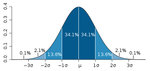
Ok, let's see on my excel file:
View attachment resampling_trades_so_far_20120112-20120224.zip


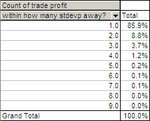
(table replaced later, once I noticed the mistake I had made, on not using the average of the population to calculate standard deviation)

Damn! If I count the drawdowns I should also count the drawups because we're really counting where it goes before returning to zero. I can't quite get it, but here we're only measuring falls and not rises and this might be what's interfering with calculating the right standard deviation and right distribution. However, if we're seeing zeros instead of positive values, then we can always verify the standard distribution by looking at the other side, which can also be done with the z-scores table:
Z Scores Table

Ok, so basically what shows as 67.4% is not, as it would appear, very close to the normal 68% (all cases within one standard deviation), because it also includes all the cases of "drawups" (as opposed to "drawdown"), which, according to the normal distribution should amount to 68% plus half of the remaining 32%, for a total of 84%. So here the distribution does not seem perfectly normal.

Damn! What a moron... I can't calculate the normal distribution, because it's based on the standard deviation, but that cannot be computed properly unless I have the drawups values.

No, wait. Wait.

Here I am only after the max fall (biggest drawdown after the entry on a given trade) and so this definitely can be calculated as simply the fall, and if the fall is zero because instead of falling (like in most cases, since the systems are profitable) it will rise, then it can be calculated normally.

But then my question is the values... ok the standard deviation which is close to the average absolute deviation (clearer concept to me) is 1500 dollars. So my question is why do we not have a negative one? I mean, all the values are positive, because i made the falls positive values (but there were no positive values to turn into negative). I mean everything seems correct, but in the bell shape aren't we supposed to have a negative half?

This would happen with trades for example (cfr. recent post on st.dev. and trades from my systems), but why doesn't it happen here?

Is it ok to do it without it? It seems to me that it's ok. Because we have the standard deviation of 1500, but what seems wrong is that you don't have negative values and so... but wait this is like those examples for ages at the zoo, that khan was doing on his web site:
Empirical rule | Khan Academy

The lifespans of anteaters in a particular zoo are normally distributed. The average anteater lives 16.5 years; the standard deviation is 3.9 years.
Estimate the probability of an anteater living longer than 20.4 years.

Ok, this is great, because if the anteater cannot live negative years, then... it's ok for my drawdowns to not have any negative values. But wait. I was seeing that 16.5 minus 3.9 leaves room for more than 4 negative standard deviations, but it doesn't have to be symmetrical because there's four on the left but there's several more on the right, since an anteater could live 80 years, but not less than zero.

Ok, so it should be ok for my drawdowns to be just deviation below and... oh ****. I forgot to calculate the mean! That's what I was missing. "The average anteater lives"... reminded me of it. I was just assuming that the average drawdown corresponded to 1 standard deviation.

I think i might have made the same mistake on that previous post i mentioned, too.

Anyway, I just went and replaced both the zipped excel file and the table snapshot. I think now it's correct. Whatever it turns out to be, whether wrong or right, there is only a slight resemblance to normal distribution, because a lot more of the population is within 1 standard distribution, and it is heavily skewed right, due to the fact that there are no negative drawdowns (of course they're all negative money, losses, but i turned them into all positive, for practical purposes - at any rate it would have been skewed left otherwise).

This is just like for trades (despite my approximations and even mistakes), as there is a great bulk of trades and drawdowns in the neighbourhood of zero, which crams within one standard deviation almost 20% more than what it should have.

---

The very good thing I did in this post though, is finding out how good my present systems are and how likely they are to blow out.

I am so exhausted in general that I don't know if I'll be able to retain anything else of what i've done here. I am totally burned out. I really need to take seriously this idea of relaxing. It has to happen now before it's too late.

 

[Yamato]

Paul Wilmott

Pretty funny how these guys are asking him questions and they have no idea what he's talking about... so they keep on trying to make it simple and get a quick simple answer from him... but they're just on a different wavelength. It's hilarious. It seems like the only purpose of the channel is to give stock tips and if you are a guest and don't do it, you're considered a pain in the ass. They don't care that you want to talk about something else: the bottom line is that you have to give a stock tip.

Paul Wilmott on CNBC 2009-09-02 - YouTube


I was looking for more videos on the kelly criterion, and I came across this video by Nathan Whitehead, very well made, on a chapter of Paul Wilmott on Quantitative Finance:

Paul Wilmott on Quantitative Finance, Chapter 17, Kelly criterion - YouTube


So I looked for the book, because it seemed very well made and I got some info on him which seemed very reassuring and promising...
Paul Wilmott - Wikipedia, the free encyclopedia
Wilmott | Serving The Quantitative Finance Community | Home
Wilmott | Serving The Quantitative Finance Community | Forums
Wilmott, Paul - Wilmott Wiki
Mathematical finance - Wikipedia, the free encyclopedia

...and sure enough I found the book, too, which somehow reminds me of the holy bible:
http://www.ps.uci.edu/~markm/numerical_methods/w.pdf

And I am going to stick it in my list of books to read. This is the biggest one - 1400 pages.

Here's another interesting summary or rather just comments on a chapter from the book, always a video by Nathan Whitehead (awesome work):

Paul Wilmott on Quantitative Finance, Chapter 20, Technical analysis and microstructure modeling - YouTube

Awesome video, by Nathan. Amazing how clearly and coherently he explains the whole material I've discovered on my own mostly during the course of ten years. Only doubt I have about this video, is when he says technical analysis doesn't work at the start (and at the end, too) and then he goes on to explain it. But what more could you ask from a person than to explain so clearly something he doesn't believe in? Also, the drawings and the colors are very clear and artistic. I think instead of trying to read the 1400 pages, I'll start by watching these wonderful videos he made (dozens of them, on as many chapters):
NathanWhitehead's Channel - YouTube

This is a fascinating world, mathematical finance. I am barely venturing into it, and never will come out alive, but I admire all these intelligent and unknown people (yeah, despite winning a nobel prize sometimes) who are doing their best in this field: kelly, thorp, markowitz... all of them. They're so much better than the regular traders, who just say "long here" and "short there". Of course, the traders might even make more money, like bill gates might make more money than some other better programmer. But their work is about intelligence, and I've got little, so I cannot help but admire them.

I wish I didn't have to go to work every day with these idiots, and could stay home and delve deeper into these subjects. Damn me, for wasting all my capital, and being forced to work for the rest of my life.

 

[Yamato]

Jobim: Chega De Saudade - Dúo del Sol - violin & guitar - YouTube

These guys are good:
DuoDelSol's Channel - YouTube

 

[Yamato]

"quant" forums

One necessary premise: I do not like the term "quant" at all. I've seen it used by superficial people in a superficial and sloppy way, so I will use the quotation marks and write "quant", because I still need to use it, given that it's so widespread that it needs to be used, even though I do not like it. I always do this, when I do not like a term, I enclose it in quotation marks (I must have done it before for "weird", "cool", "loser" and "winner").

So, on to these "quant" forums. Not that I'd ever dare to post there, but it might be interesting to take a peak every once in a while. Getting the idea from Wilmott forums, I have done a little research and found another similar forum, specifically meant for mathematical finance (aka "quantitative finance", aka "financial engineering", aka "computational finance"), so let's look at them both:

QuantNet Community
Wilmott | Serving The Quantitative Finance Community | Forums

These forums are very scary to me, because it makes me wonder how can I be making money to begin with, and how long can it last, when I am up against thousands of these people, who at 10 years of age were better at math than me now.


browsing through the "quant" forums

I am going to dig up some interesting threads from those two forums and will post the links here.

Trading vs. Quant Research | QuantNet Community

I was thinking that trading is more hands-on and sometimes doesn't require so much quant stuff. Like for example the algorithms are already all there, you just have to be the human watching over them and making hundreds of little (non-quant) decisions a day.

Perks: money. And lots of it.
Cons: Traders get fired. Societe Generale in France got rid of the vast majority of them, and UBS firings have been just out of the ballpark. Also, if you haven't used your quant education in everyday life for years now, you've probably forgotten a lot of it: the models, the calibration methods, stochastic calculus and PDE's. It's a shame because not a lot of people are good at those things, and you used to be.

Another way to think about it: A quant with years upon years of experience can always get into trading. That door is always open. But an experienced trader can rarely pass the technical exam to get into quant research.

Yeah, good point. No ****. The only reassuring thing I read is "not a lot of people are good at those things".

On Wilmott's forum, the one interesting forum section to look at is this:
Wilmott Forums - Jobs Board
No need for me to commento: it speaks for itself. Once again, I feel scared.

I will not learn much math by taking a look at these forums, but I'll get a rough idea about how ignorant I am, and what I might be missing, and what can be achieved. It's useful information, even just knowing what you ignore.


"portfolio" string search on "quant" forums

Now, a good question would be: what do these guys say about portfolio theory? I am going to do a search.

Search Wilmott Articles & Forums
Search | QuantNet Community

Because, I mean, a thread on portfolio theory by these quants, who have read it all, might save me a lot of time on what I need to cover.


Wilmott

From Wilmott Articles Search:
http://www.wilmott.com/detail.cfm?articleID=278
http://www.wilmott.com/detail.cfm?articleID=151
http://www.wilmott.com/detail.cfm?articleID=138
These I cannot read yet, because i need to be logged in, and they have to review my registration first.

From Wilmott Forum Search:
Wilmott Forums - Merton's portfolio problem - why dying rich?

Leaving your kids money in no way guarantees that they won't pee on your grave, or even visit it.

Not that I have this problem right now. The present situation is living poor and dying poor, or even from poverty.

Wilmott Forums - Markowitz Portfolio Of The Week
Wow, quite odd. I cannot read the articles unless I am a registered member of the forum, but I can read the forum threads, and even download the attachments (this is an interesting attachment, from the last post of the thread linked):
http://www.wilmott.com/attachments/ExSan_V.4.01.S_Markowitz_Portfolio_Automata_4.6_16.zip

Following ExSan trail... (not from wilmott but user found on wilmott):
Markowitz Portfolio Automata Handler ExSan3.18.U

Links:Tutorialseltaquants

An Introduction to Computational Finance Without Agonizing Pain
(this is still totally agonizing pain for me, but chapter 11 is all I need)

Back on the wilmott forum:
Wilmott Forums - Kelly Criterion Applied to Portfolio Construction

Hi All,

I am an absolute beginner in the quant arena and wanted to find out information on applying the Kelly Criterion to portfolio construction the portfolio being composed of hedge funds.

I have searched on google but most links talk about Kelly applied to gambling and a few are there touching Kelly's application to finance but not in detail

Could you please point me to some information sources where I can learn in detail about how Kelly can be applied to portfolio construction

Lots of references here: Money Management

I told you the other day that Sewell seemed to be a smart guy. Actually this is the best link and maybe only essay on the history of portfolio theory. I wrote myself an email and tomorrow I'll print it at the office so I can read it on my cab ride to work and can ride home. To summarize you need to synthesize and simplify and these mother ****ing academics rarely do it. Actually they make an effort to keep knowledge over-complex and labyrinthine. Thanks, Sewell.


QuantNet

Who are the top Quant consultants on Portfolio Construction | QuantNet Community

Who are the top Quant consultants in portfolio construction space who are experienced in advising fund of funds and pension funds? We were recommended SortinoDTR, who seems to be focused on the long only space. Who are the others - particularly those who specialize in dealing with Quant and Hedge Funds? Where can I find a list of top consultants? What has been the experience of forum members with some of these consultants? Thanks.

Wow, to judge by this question (unanswered), the members of this forum are quite important.

Portfolio Optimization | QuantNet Community

AlgoCan
New Member

Hi all,

Can anyone share experience or pointers on portfolio optimization tools/softwares especially for institutional asset management?

Appreciate your help

...

Andy Nguyen
Member

Attilio Meucci runs a group on LinkedIn that you may find close to what you need
SYMMYS - Advanced Risk and Portfolio Management | LinkedIn

Wow, very advanced discussion on LinkedIn. I am totally clueless as to what they're talking about:

I confess I am charmed by the speed and elegance of the entropy-pooling approach. In Meucci's paper "Fully Flexible Views - Theory and Practice" paper it states in the Introduction: "The output [of entropy pooling] is a distribution, which we call "posterior", that incorporates all inputs and can be used for risk management and portfolio optimization." Exactly how does one perform asset allocation based on the updated probabilities for the various joint-scenarios?

Well, no wonder:
Attilio Meucci - Resume | www.symmys.com

Education
»CFA, CFA Institute 2003
»PhD Mathematics, University of Milan 1999
»MA Economics, Bocconi University 1999
»BA Physics summa cum laude, University of Milan 1994

I mean... until recently I was held back in both highschool and college due to sucking at math, and here I am hoping to figure out what this guy says.

These "portfolio" search hits are many more and much closer than those found on wilmott forum. But I am noticing most forum threads do not receive any replies, whereas on wilmott, most threads got answered. I wonder why. Considering these are all good threads.

Free online tool to perform portfolio optimization and sensitivity analysis | QuantNet Community

I already mentioned this to someone, so I might as well start a new thread about it.

Have a look at this: Professional portfolio management and reporting tool

It is a free tool with which you can create reports, perform Markowitz type mean-variance portfolio optimization and conduct sensitivity analyses. Sensitivity analysis here refers to assessing the effect of +/- 50% change in exposure to a portfolio component in terms of the overall risk-return profile of the portfolio.

The security data is free EOD, and it covers the US stock markets as well as the major ones in Europe, Asia, South America and Australia.

I had built something like this in Matlab a long time ago for personal use and found it rather useful for keeping my long-term portfolio on track. Having recently familiarized myself with server-side programming, I decided to put it available for the public. I hope you find it useful.

No replies again.

Ok, this interview is great (the thread is just a link) - I am gonna have to print it:
Five Good Questions on Portfolio Theory with Hedge-Fund Manager Scott Vincent | QuantNet Community
Five Good Questions on Portfolio Theory with Hedge-Fund Manager Scott Vincent

I'll stop here. Hopefully I won't forget about these two forums, even though right now it's mostly greek to me. I don't know enough math to understand what 90% of the threads are talking about.

The QuantNet forum interface is awesome, better than anything I've ever seen before. There's even a "keyword alert" utility, that sends you an email if there's new threads with a certain keyword.

 

[Yamato]

need for formula literacy

Portfolio theory all boils down to formulas, there's no way around it. When I first looked at Markowitz's 1952 paper, I thought he was showing off, to impress someone, for his thesis, and I figured that's why he used all those formulas. Nonetheless, I felt the urge to study math.

But after all the math I've been doing, I only understand them a little better. The more important change is that I do not run away from them. It's like when I was learning English, in the first few weeks of full immersion in the US. After a point, I was understanding enough to realize that I was going to make it, and finally learn the language. I am at that point with math and formulas.

And, as I kept reading portfolio theory books, I found that for sure, Markowitz was not showing off - it was simply the first such book I had come across, and all of them portfolio theory mother ****ers use the same amount of formulas. Unfortunately it's not the same formulas I've been practicing on Khan Academy.

So I've done a search on google to find a tutorial that would help me become fluent in mathematical formulas in general, but I could not find anything. This is a problem I have to solve. It's just like learning a foreign language, except I don't know exactly where I should travel to learn this language through some sort of full immersion. In the meanwhile, I'll just keep hanging out on these books, even though it reminds me when I was 14 and I rented movies in English and i was trying to understand them, but I never achieved much, and pretty quickly I got discouraged and quit. It was only 4 years later when I went to the US to study, that I finally learned it. I wouldn't want the same thing to happen with formulas: trying something so hard that it makes you quit. In other words, I do not think I can become proficient in formulas by reading these books in my signature. I'd probably just keep picking them up, several times, and each time understand a tiny bit more, but also I'd get each a tiny bit more discouraged, and I'd eventually quit due to the impossible learning curve. Even mathematicians did not become mathematicians by being given formulas from the start.

 

[Yamato]

I got into the umpteenth argument with my Italian friend, the one I tutored on trading systems, who keeps on asking me to take his capital. As usual, when things are working out, everyone starts being interested - but it's always too late. Then, when it doesn't work out, no one is interested - which is when you'd need them. There were six people interested in giving me money when I was busy with the investors, until late september. Then, a month later, after we stopped, no one was interested anymore. So I had to save and start all over again, by myself. Now this guy is interested again.

But he's a pain in the ass. At the start of January he wanted to negotiate and bargain, so I told him my conditions were not negotiable, and we stopped talking for a month. Now he's been proposing more deals, increasingly favorable to me (not logging into my account, not wanting to see the trades, etc.), but I've had each time to decline, because now I don't need his capital anymore. And then, each time I refuse, he gets upset, "disappointed" and similar. So I always tell him in advance "let's negotiate, but no fights if we don't reach an agreement". I did this time, too, but it didn't work and he wrote me a hate email, ending it with "let's meet tomorrow so you can fix my excel problem".

I'd feel like saying "i am not taking this crap from you and then meeting you to help you with excel", but you never know what the future holds - I never really split with anyone. So tomorrow I'll help him and then, as usual, block his email and block him on skype, so he doesn't bother me until he calls me on the phone, which will probably take him a few months. I am so glad I didn't start any business relationship with this guy. He gave me a taste of my own medicine - he's a highly neurotic mother ****er, who writes hate emails. Just like I do. It's impossible to have any sort of relationship with this guy. Because he's identical to me.

 

[Yamato]

youtube videos on mathematical finance

At this point, the easier and most effective path for me to take is to watch youtube videos (mostly lectures) on this complex subject I am tackling. They're easier than plain formulas, easier than books (which are half written through formulas) and they're very long, abundant and well made.

Here's some:

Two dozen videos here:
NathanWhitehead's Channel - YouTube

Seven videos here:
kmpetrov's Channel - YouTube

Four of them here:
economicsnetwork's Channel - YouTube

This is good, too:

Some Applications of Mathematics in Finance - YouTube


Then there's Simon Benninga at TAUVOD:
TAUVOD's Channel - YouTube

Lecture 2: Computing Efficient Portfolios - YouTube

Lecture 1: Portfolio Choice with Multiple Assets - YouTube

Lecture 3: Black-Litterman Model - YouTube

 

[Yamato]

back at the office

It's going pretty swell, considering that my colleague ain't here - he's gone for a surgery. Away all last week. Just as I wished. I wished him a long stay at the hospital and a slow recovery and it happened. The god of randomness has fulfilled my wishes for peace, and I am doing great, here all by myself.

In the meanwhile, I've been monitoring the NG and QG contracts and finally QG has stopped trading but NG is still alive and kicking:






Oh, and let's mention that a short on GBL looks more promising than ever:



It rarely reached these levels, and it's clearly having problems getting above 139.

This is my type of trade, where it just can't go any lower (NG) or it just can't go any higher (GBL). Where are these guys gonna go? Can NG go below zero?

Astor Piazzolla - Otoño Porteño (Live in Montreal 1984) [HQ] - YouTube

 

[Yamato]

Five Good Questions on Portfolio Theory with Hedge-Fund Manager Scott Vincent

As I said yesterday, being at work, I printed this interview with Scott Vincent, and I am reading it, but this is so good, and so related to what I am studying, that it needs to be quoted here, so I can also write down my comments:
Five Good Questions on Portfolio Theory with Hedge-Fund Manager Scott Vincent

1. In your recent paper, you argue that modern statistical finance isn’t all that it’s cracked up to be, and that active management can and does work. On what do you base those conclusions?

The fundamental underpinnings of quantitative finance have been shown to be flawed and impractical as applied in practice. Most of quantitative finance depends on the basic concepts and statistical math introduced in CAPM and Portfolio Selection (two of the key theories behind Modern Portfolio Theory or (MPT). We tend to assume that because these theories appear sound, and the math behind them is flawless, they will generate accurate results when applied.

[...]

This guy knows his ****. Concise and to the point. That's what my father was saying last night: just because these "quants" are so good at math and their formulas seem to be flawless, it doesn't mean using those formulas is appropriate. They might be based on the wrong assumptions. My dad was telling me that lately, the scientific specialization is so high that you don't have a figure who knows the whole thing any more (because it's so hard to know everything), someone who can see the big picture, so the math guys (at least not ALL the math guys) may not know enough about trading to get the right results. And the other guys who know what's needed may be feel too insecure to tell anything to the "quants", and if they do, in a company, they might be told "hey, what the **** do you know about math? Then shut up and listen to this scientist".

Anyway, who is Scott Vincent and what's this paper they're talking about?
...

Nice website, with nothing in it:
GREEN RIVER, LLC

There's more here:
Scott Vincent

Mr. Vincent has over seventeen years of experience in the financial services industry including positions in portfolio management, institutional equity research sales, and investment banking. He earned an MBA at Georgetown University, and a BA in Economics at Kenyon College.

So ok, he didn't do a lot of math in his life, and that's why he sees the big picture maybe, or maybe he doesn't appreciate these formulas too much because he's not into formulas. Let's keep this in mind as I read.

The paper is here and I've just printed it:
Is Portfolio Theory Harming Your Portfolio? by Scott Vincent :: SSRN

But first I'll read the rest of the interview.

Of course, I'd have liked it better if, for a change, a Ph.D. in math had said "all these formulas are useless", instead of an MBA telling me the same thing.

Another good quote (from the interview), which summarizes his view:

MPT's assumptions don’t square with reality, so we shouldn’t be surprised that its key concepts don’t hold up when put to the test in financial markets.

The misapplication of financial theories gives us a precise measure of risk, which imbues us with a false sense of security and allows us to build very large portfolios. Yet when the predictably unpredictable happens, and correlations break down, we realize -- too late -- the mistakes we’ve made.

This also reminds me a little bit what happened with the investors. Flawless application of the wrong formulas.

We don't have the space to address the issue adequately right here, but it's interesting to ask, Why do our capital markets continue to embrace quantitative finance so enthusiastically, despite its widely acknowledged shortcomings? And what are the ramifications?

I think the short answer to the first question is that we have a lot vested in our financial system that depends on quantitative finance.

With respect to the second question one can argue that the result is massive inefficiencies and misallocation of capital. I think that an overreliance on quantitative finance played a big role in causing the recent financial crisis. Anyone wishing to learn more should read Amar Bhide's book, A Call For Judgment.

I'd like to know what he exactly means by "a lot vested in our financial system that depends on quantitative finance".

Diversification allows funds to achieve massive scale and profitability, even if it may prevent them from offering real active management (where managers take large positions in select names) and superior returns.

3. How do you get along or make peace with quants, who get some serious criticism from you?

There will always be a place for quantitative finance. We’re not trying to argue that the models don’t work in theory. We’re saying that they are misapplied in practice.

If all the assumptions that the models require hold, then they generate a fairly accurate picture. So, in some circumstances, the models can give a helpful reference point when analyzing a security. It’s when they provide the sole or primary reference point that we get in trouble.

Even though the facts are stacked against them, the quants aren’t in any real danger of losing their jobs. As mentioned earlier, we've built a financial services system around the idea that quantitative finance works. That system depends on quantitative finance for its life blood of profits.

Quantitative finance also has the benefit of defining the debate over its validity using terms that presuppose the validity of the very theories over which we argue.

How can we deliberate about risk-adjusted returns, Sharpe ratios, or alpha fade when those terms rely on bogus assumptions? The measuring stick is broken but we keep using it.

I don't know if I totally agree with this. The individual systems I trade can be measured with the sharpe ratio, because even if it might be unreliable, all other things being equal, it is still the most reliable way to measure different systems. I can still tell by using it, which system is better, all other things being equal. The trouble can happen at any time with any system/future, but, all other things being equal, a system with a high sharpe ratio is better than another system with a low sharpe ratio.

...But given that I’m a stock picker, the people who help me most are analysts who have a deep understanding of the companies they follow, who don’t take management at their word, and who understand not only what makes a great company but what makes a great investment. I’ve gotten to know a lot of outstanding analysts over the years and I’m privileged to count many of them as friends.

This guy invests based on fundamental analysis so some of the things he says do not apply to my type of investing, because statistics matter much more (since they're more reliable) for my field (automated trading) than for his field. I will still try to read his paper now.

 

[Yamato]

my GBL short trade

Damn, I have to admit that my GBL trade, short from 139, is not looking good at all:
Eurex - Fixed Income Derivatives



But I can still hold it (losing 500 euros is heavy but I can still take it) and how long more can this guy keep on rising? At any rate, there will be a reversal tomorrow, even if it rises today, because that's what tends to happen.

Then tomorrow, if I can close it at breakeven, I might just do that. Because this thing is about to expire and I wouldn't want to close it higher.

 

[Yamato]

Is Portfolio Theory Harming Your Portfolio?

Continuing from here:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-63.html#post1798624

Actually I am reading Scott Vincent's paper, from here:
Is Portfolio Theory Harming Your Portfolio? by Scott Vincent :: SSRN

The paper starts like this:

Modern Portfolio Theory (MPT) teaches us that active equity managers who use judgment to make investment decisions won’t be able to match the returns (after fees and expenses) of blindly-invested, passively-managed index funds. Data on returns supports the theory, so it’s no surprise that investors are leaving actively managed funds in droves for the better average returns of super-diversified index strategies. Yet the reality is much murkier than we’ve been led to believe.

And I realize that I've forgotten to spot a major difference: I am an active manager. I am indeed looking for portfolio theories to help my management, but, given that I have a portfolio of trading systems I am not exactly the target audience of Modern Portfolio Theory.

I am still wondering if I can consider a trading system like an element of a portfolio to "passively manage", or instead if it's like a very actively managed portfolio. There's definitely something to think about here, but I am clearly neither within the realm Scott Vincent belongs to (fundamental analysis of stocks to pick) nor the realm of markowitz's Modern Portfolio Theory (create a diversified portfolio of assets, with the right proportions, and don't worry about it).

I am something in between, but I agree with what Scott Vincent will probably say: that good active portfolio managers are capable of outperforming passive portfolios. But what markowitz said, even in a youtube video I recently watched (posted on my journal 2), is that, for average people, it's best to do things his way. Then for the super-expert things are different, so i can agree with him, too. Because, for example, I would probably lose money, too, if I engaged in stock picking.

[...]

Ok, back at home.

I've been reading on the cab ride home and I figured it out. Modern Portfolio Theory is not necessarily wrong, but it has to be interpreted and what is wrong is the way it's being interpreted by many.

I still don't know much about it, but from what I've read, it basically suggest a diversified basket of different investments, based on their performance as measured by the sharpe ratio.

So, with these premises, my question is: who says that I cannot treat my systems like markowitz prescribes (provided I understand what the **** he prescribes in detail, because his formulas are still Greek to me, actually worse - Arabic) and have a diversified portfolio of systems?

So this would agree with both the passive and active management concepts, because my systems are definitely active managers, but I would be passively trading them.

On the other hand, I do not know if markowitz's theory would agree with what Scott Vincent does and suggests, which is picking a few things, the best ones you can find.

So, I don't know who I agree with, and if I am taking the best of both maybe. Because as i said my systems definitely qualify as active management, as Vincent would want, and they also definitely aim at overperforming all the benchmarks, like Vincent wants, but on the other hand I do want to diversify as much as possible, and I do believe in sharpe ratio and the many statistics I have available from my systems.

So maybe he disagrees with Modern Portfolio Theory, but I don't disagree as much as he does, and maybe I don't disagree at all.

Of course, when I'll read the rest of his paper, I'll have something more to write about all this.

[...]

Ok, I read a few more pages, and the guy writes pretty clearly. I like him. Finally something simple enough for me. It lacks a bit in structure, but it more than makes up for it with clarity and conciseness.

I have to quote this awesome summary of modern portfolio theory:

History

We can trace the beginning of our fascination with the idea of passively managed funds back to 1952. That year, a student of linear programming, Harry Markowitz, first applied his craft to the world of finance in a paper entitled “Portfolio Selection.” In it, Markowitz provided mathematical proof that proper diversification could minimize a portfolio’s variance for a given level of return. Mean-variance was used as a proxy for risk because assets whose prices were more volatile were seen as more likely to produce losses. It was the first time anyone had formally quantified this tradeoff between risk and return. Paying special attention to how an asset’s returns correlated with other assets allowed mathematicians to create groups of portfolios which minimized risk for a given level of return, or that maximized return for a given level of risk. These large, mathematically optimized portfolios formed the “efficient frontier” and helped inspire today’s highly diversified, passively managed funds.

“Portfolio Selection” spawned William Sharpe’s “Capital Asset Pricing Model” (CAPM),4 which made Markowitz’s work more user-friendly. CAPM introduced “beta,” a measure that incorporated a security’s variance versus an underlying index (rather than vs. every other security in a portfolio), and that represented systematic risk. The name of the game according to CAPM was to diversify away stock-specific or idiosyncratic risk leaving only market (systematic) risk, which was defined by beta. According to the theory, investors are foolish to hold a small number of stocks because they’re taking stock-specific risk when they don’t have to. Since other investors are buying the same securities in diversified portfolios, the non-diversified investor will bear more risk for equal return and therefore pay too much for a given stock which is priced for inclusion in a diversified portfolio. A portfolio should be optimized in a manner such that it has the lowest possible risk (beta) for a given level of expected return which in practice means holding the market portfolio and lending or borrowing to adjust risk.

Finally, the “Efficient Market Hypothesis” (EMH) was introduced in 1970, by Eugene Fama, in the form we’ve come to recognize. Providing what some call the capstone to modern portfolio theory, the efficient-market hypothesis asserted that because the stock market is such a successful mechanism for pricing securities it is difficult or impossible for an investor to achieve returns above the market average in any consistent fashion. Prices reflect all relevant information, and changes in securities prices are mostly unpredictable, so using judgment to pick stocks may be ineffective in the long-run.

Fama named three versions of EMH – weak, semi-strong, and strong. The weak version holds that past prices don’t predict future prices, so technical analysis (which is based on past trading information) is irrelevant. In the semi-strong version all publicly available information (not just price information) is instantly discounted in stock prices. And in the strong version, even non-public information is discounted such that insiders wouldn’t be able to profit consistently from trading around their knowledge.

The three theories -- EMH, CAPM, and Portfolio Selection --were classified together as “Modern Portfolio Theory” (MPT). They were so compelling and useful that they came to provide the backbone for much of modern financial economics and earned both Markowitz and Sharpe Nobel prizes. They were identified together, built on one another, and became joined in practical expressions. And although they each got there taking different avenues, their conclusions were much the same – buy the market basket.

In fact this is the most interesting topic for me, and I've found a similar summary in that other work, this time by Sewell, that i've also printed and am planning to read:
Money Management

That's the way you should always begin, but with this subject it wasn't easy to find what I wanted to read.

Actually I had found a little bit of history and written about it in this post:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-56.html#post1794498

 

[Yamato]

Ok, IB finally fixed the security prompt problem (cfr. my previous posts complaining about it):
Forums - IB TWS security token asked after disconnection

I have to remember to give them a new rating, that keeps into account the improvement they made:
http://www.elitetrader.com/br/?action=view&R_FirmID=43

 

[Yamato]

I am improving

Ok this is pretty good news.

I am losing on both of my "top/bottom picking" trades:


And the good news is that when I was writing "my journal" in 2009 and "my journal 2" in 2010 e 2011, I would have felt the irresistible urge to double up on my losing positions.

Today instead, first of all I know that it really can't go much further, and that's why I am not desperate to begin with, but second of all I did not feel that urge. I just remembered that I used to feel this urge to double up. So I came here to write it. It's a journal after all.

I don't feel like doubling up because I know that these two futures can't really go that far, and yet that the only way I could blow out my account is precisely by doubling up.

Maybe I know that I can make money by waiting rather than by doubling up and hoping for a small bounce. This is because I know that they didn't get away from me, and that they're not going anywhere. They're coming back, because there's really nowhere to go from the levels they're at right now.

Yes, ok: natural gas can go to 1.5, but then I'd just lose 3000 dollars. That's what makes me relax.

 

[Yamato]

more videos on portfolio theory and mathematical finance

Continuing from here:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-62.html#post1798418

In random order this time. Need to investigate more in the future.

Stock market simulation | MIT Computer Science Lecture

Financial Markets | Yale Video Course

Portfolio Diversification and Supporting Financial Institutions (CAPM Model) | Yale Entrepreneurship Lecture

Financial Markets Online Course, Yale Economics, Robert Shiller | Free Video lectures, Download

This last one is good (teacher is good), even though it doesn't seem too related to portfolio theory:
Financial Theory Online Course, Yale Economics, John Geanakoplos | Free Video lectures, Download
Yeah, I need to watch this, too. It is pretty much... "fun". Better than audio-books (which I could never find on portfolio theory). And at worst, I'll fall asleep, as I need to do.

Awesome, awesome, awesome.

 

[Yamato]

I thought I'd have the best of both worlds, discretionary and automated, and so far it happened and I made 2000 more thanks to discretionary. But this edge is slowly being eroded, because mistake after mistake, discretionary is taking its toll.

GBL and QG trades weren't that intelligent as I was thinking. Yes, they don't seem to have a lot of room for going against me, but there's contango (as mentioned in ealier posts) and there's the fact that I need the margin they're using. So, they weren't as stupid as most of my trades, but they were still stupid.

Last night for example, GBL and QG were using up all the margin, and so the NQ automated trade didn't go through, and today I missed out, so far, on 200 dollars of profit.

Discretionary benefits from intelligence and flexibility, but distraction and impatience in conjunction with flexibility is what hurts it. You make mistakes you could have avoided, because it's not easy to remember all the types of mistakes you could make, blinded as you are by your desire and hope to make money. In other words, a perfectly alert and infinitely patient machine, in the long run, works better than the person who created it.

It's indeed an awful situation, because I can't get to accept this fact of being worse than the machine that I created.

And I don't know how much room there is for learning, given that your judgment is clowded by your hope to make money. So that is why, once again, full automation is the best thing. But listen to this catch 22 situation: to achieve full automation you must stop having a life, and if you stop having a life, you're going to have a lot of free time needed to achieve full automation, and yet once that happens, having a lot of free time gets in the way of not tampering with your systems. So basically now i have to get back into a social routine, which I have learned to consider a waste of time. The only purpose of it seems to be to stay away from tampering with my systems. That right now seems the only thing I will achieve by meeting with people, and going to the movies or to a dinner.

 

[Yamato]

more on scott vincent

Continuing from here:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-63.html#post1798734

I am still reading Scott Vincent's paper, "Is Portfolio Theory Harming Your Portfolio?", and I found something really worth quoting on page 7, which sums up what he's been saying in the previous pages:

That these quantitative financial models don’t work in practice isn’t controversial. The theories have been losing the battle in scholarly articles for the last three decades. Even many of the influential researchers behind modern portfolio theory admit to their shortcomings. Markowitz is quoted as describing his book on Portfolio Theory as “really a closed logical piece” – i.e., something that only works in the lab. Eugene Fama called CAPM “atrocious as an empirical model” and said “CAPM’s empirical problems probably invalidate its use in applications” Fama & French (2004). Even the ardent supporter of EMH, Paul Samuelson, noted "... few not-very-significant apparent exceptions" to micro-efficient markets, and admitted the existence of some exceptionally talented people who can probably garner superior risk-corrected returns.

The real controversy is that, even though its chief architects admit the quantitative theories are ill-suited for practical use, and empirical data confirms it, they are still embraced,(indeed some might say “worshipped”) by operators in our capital markets, and heavily relied on to make important financial decisions. The theories have become so deeply ingrained in our financial system that we can’t see their folly. Their mathematics, as well as the precise nature of their output, gives us a sense of comfort which is critical in deploying large sums of money. They also lead to a misallocation of resources, however, causing giant distortions.

[...]

Luckily, my roommate still didn't come back from the hospital, so I am still reading peacefully and I got to page 10 included. In the meanwhile GBL and QG are doing okay and it would seem that soon they'll go where I want them to go.

Now I need to quote something and reason out loud, by writing about it, because the amount of information and opinions he's giving me might not stick with me. I need some reasoning.

Over-diversification not only decreases a manager’s ability to find inefficiencies but it may, in fact, increase risk. Warren Buffett expressed the idea more eloquently, “We believe that a policy of portfolio concentration may well decrease risk if it raises, as it should, both the intensity with which an investor thinks about a business and the comfort-level he must feel with its economic characteristics before buying into it.”14 Over-diversification inhibits a manager’s ability to understand the risks taken with each security, potentially creating greater risk. This argument turns CAPM on its head. A highly diversified, active manager cannot fully understand the risks he is taking on his positions so he may be paying too much for them, thus operating below the efficient frontier.

This pretty much sums it up, and in fact the author is repeating himself quite a bit, due to a lack of structure I mentioned in earlier posts. I would derive from his reasoning this conclusion. You either totally quit stock-picking and buy the indexes (ETFs or whatever they're called), baskets with ALL the stocks in it, and you mix them according to markowitz's formulas. Or, as the author advises, you engage in active management and in that case diversifying is still good, but you cannot diversify too much or you won't be able to weigh your choices carefully enough. Maybe what the author is getting at (but never states clearly) is that nowadays, being diversification so popular, many fund managers make the mistake of not diversifying enough to be following the passive management prescribed by MPT, and yet they diversify too much to be able to pick the right stocks.

[...]

I am now on page 12, and I am going to repeat myself, too, probably, as the author. But this is a journal and not a paper, so I am allowed to do anything I want.

What I'll say is that the author and what markowitz says do not disagree. I may have said before. Markowitz in a youtube video I posted on my journal 2 said that, for most people, since they won't be able to pick the right stocks nor the right managers, he advises his diversification approach (basket of stocks, basket of bonds, and so on). This does not mean that he says that a better edge cannot be achieved. But it's not likely to happen, so he advises against trying it. We all know that the majority of traders are unprofitable, so markowitz is saying the same thing, and yet he's also saying that you can make a lot of money by simply diversifying (according to his formula). Maybe Sharpe, Samuelson and Fama took it much further than markowitz, but, judging from I heard from him on youtube, he does not rule out that some fund managers may outperform his diversification approach. But I guess we all agree: things definitely got out of proportion, as Scott Vincent says. The theory would have been ok, but the industry took it much further and misinterpreted it.

I am almost done (two more pages to go) and I am glad I read this paper. It clarified so many things in a simple language. I appreciated this paper a lot, even though it did not concern me directly. But it gave me a much better understanding of modern portfolio theory and its history.

At the same time, there are some flaws. I almost do not understand why it was written and who is it arguing against. I said "almost" because I guess after many years in the business he is sick and tired of seeing the misinterpretation and misuse of markowitz's theories. And he's got a point. And in the process of venting out his frustration, he clarified the whole portfolio management business to me.

Ok, on page 12 there's a good summarizing quote again:

It is ironic that while the financial services industry and investors have spent the last thirty years rushing after the quantitatively inspired ideas of Samuelson, Markowitz, Sharpe, Fama, and others, academics, on balance, have been running in the opposite direction -- relentlessly throwing into doubt the underlying tenets of quantitative finance. Moreover, Samuelson’s flawed Challenge was met and returned with the brute force of empirical results from the practitioners most reliant on judgment --concentrated active fund managers. Judgment pulled-off the big upset, rallied from behind to win the game, but almost no one has taken notice.

This really sums up the whole paper. Reading this would have been enough. Here's what happened. The fund managers, who generally are idiots (or controlled by idiots) are behind, the industry is behind relative to the academics, and it has embraced the misinterpretation of old scientific theories (markowitz and others), now challenged by other academics, and hired a lot of mathematicians who get paid a lot of money to apply flawlessly the right (or even wrong) formulas at the wrong time and in the wrong place.

Which brings us back to the point he made in the interview which I quoted in my first post on Scott Vincent:
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-63.html#post1798624

We tend to assume that because these theories appear sound, and the math behind them is flawless, they will generate accurate results when applied.

Always from page 12 of the paper, here's another good paragraph:

The triumph of judgment has been overlooked by most investors due to the confusion created by MPT. We’ve allowed one of the players in the match (MPT) to dictate the rules of the game. MPT’s rules not only insure its own victory, but they also create a complex web of circular arguments that inhibit our ability to discern the truth. MPT’s characterization of risk is the ruler we use for comparing active vs. passive strategies, often causing active strategies to appear more risky and less efficient than their index counterparts. The same flawed logic is used to risk-adjust returns, biasing them downward for more active, concentrated managers, and rendering this highly important measure highly suspect. Furthermore, reliance on MPT’s measure of risk pressures active managers to super-diversify. The average active fund is thus disfigured to the point where the typical “active” manager is not very active at all, casting the fund in an unfavorable light in a beauty contest versus super-efficient index funds.

There’s a feeling of safety that accompanies index investing; neither the advisor nor the investor risks losing face or losing a job over putting money to work in a broad index.

This is a point he's made before, but here he summarizes it better (he should have written everything in 5 pages, but then he couldn't have called it a "paper" and he would have been taken less seriously):

Further, moving to judgment-based finance isn’t good business for the financial services industry. The industry depends on quantitative finance to bring it scale and profitability. None of the above are valid arguments, but that’s not the point. When defending an entrenched system that furthers the economic interests of powerful entities, the rationale doesn’t need to be sound, it just has to be somewhat convincing.

Basically he says that MPT was successful because (maybe because it produces safer investments, despite the fact that it forces everyone to be mediocre) it encouraged people to invest in the markets, so if it is in the interest of investment funds to keep "index investing" popular (no matter how unreasonable), since it attracts customers. Besides, I don't really think it is unreasonable. For the average investor this approach might be better (if it's done properly), because otherwise he's not likely to pick the right active fund manager. Nor likely to be doing better by himself.

Now I am at the end of page 13:

Never before has so much money sloshed around our capital markets without the benefit of judgment.

The fact that MPT became so fashionable and widespread has shifted investments from fundamental analysis of the balance sheets to blind index investing, and this has disadvantages for the markets, where good companies do not get the capital they deserve, but it has created an edge for those who don't invest blindly. This point I can understand and agree with. The real problem with this paper is that it is spread out and diluted and takes 14 pages to make points he could have made in 5 pages, more efficiently, concisely and coherently. It's not an academic paper, but it still manages to have a lot of unnecessary things in it. However, I thank him because he taught me things by writing in a simple language.

Page 14:

Do your homework and uncover mispriced assets on your own or look for concentrated, fundamentally-driven, relatively small funds with talented managers. Since persistence has been demonstrated in this subset, it turns out that a good manager may be identified from past performance among other considerations. Find managers who fit your style and risk tolerance, and invest for long term returns. Take advantage of the fact that your neighbors are leaving for passive funds, as their passive investments could provide the inefficiency your manager seeks to exploit. But, by all means, avoid investing in highly diversified active funds whose returns closely match an index. If index returns are what you seek, then pull your money and invest in efficient passive index funds or ETFs.

The part I highlighted in red, if they listened to him, would cause ordinary people to risk losing all their money, because they're incapable of doing what he suggests. The part in green is good advice. And he would agree with markowitz. Basically he fails to clarify that they never disagreed in the first place. What matters is doing markowitz right, or not doing it at all. Anything in between is bad.

The concluding paragraph brings up to the surface all the contradictions of this paper:

Most of the wealth in the world has resulted from individual entrepreneurs using their judgment to invest in opportunities (inefficiencies) in a highly concentrated, even exclusive, fashion. Think about that for a moment, because it’s a big statement. Sure, wealth has been lost using this formula, but the good has dramatically outweighed the bad. Although far from perfect, human judgment has advanced us a very long way. While public markets are much more efficient than the entrepreneurs’ private markets, they still contain inefficiencies. Accordingly, good judgment will reward investors over time. Demoting a time-tested, highly successful system that favors judgment in preference for one supported by an unsound infrastructure of quantitative theories and formulas, doesn’t make a lot of sense. Make this flaw your opportunity.

Yeah, because, dude, who did you write this paper for? For the common people, it would seem. Well, the common people can't do what you are suggesting. If they try, they would probably end up losing 50% of their capital in the first year. And certainly they would not be able to sleep at night. So, whereas the some MPT academics, or the common understanding of MPT, exaggerate in saying that no one can have an edge better than their suggested efficient frontier, it is also true that for ordinary people, your approach does not work. So you should not have pretended you were writing this paper for the ordinary people, unless what you're hinting at is that they could try to give you their funds, because you're the one capable of "making this flaw your opportunity". I don't think so, because there's nothing on your website (just a homepage) and I don't see any self-promotion in the rest of this paper, so I just think your paper is incoherent in some parts. But thanks for your clear writing style.

Before the post expires, I must add a related link, on the concept that diversification might be overrated:
Lecture in Portfolio Theory Video Lecture, London School of Business and Finance Business Management videos | Free Online Course

[...]

Now on to the next reading:
History of Money Management

This webpage is by Martin Sewell, whom I already wrote about here (he's got a wonderful website about trading systems and portfolio theory):
http://www.trade2win.com/boards/trading-journals/140032-my-journal-3-a-60.html#post1797584

[...]

Back at home.

Wow, this is awesome. Sewell has read all the books on portfolio theory and he's summing up all the knowledge I was missing. This is a gold mine. I will have to finish it first and then later I'll write a thread on this wonderful page. Probably the best resource i've ever found on portfolio theory. I'm going to place it in my signature.

I need to memorize every single sentence he wrote and investigate his references.

 

[Yamato]

March contracts of QG and NG are history

Today, finally, for the first time, those QG and NG March contracts that I've been monitoring, are totally gone from the two CME pages (no need to quote QG, because it was gone as of yesterday):
Henry Hub Natural Gas

 

[Yamato]

more on martin sewell

In the bath tub I read all of Martin Sewell's history of money management.

By the way, a few minutes earlier, before the bath, I've opened another short position on GBL, which is something that just yesterday I was boasting I would not do anymore, because I've matured. I was wrong.

Martin Sewell's concise history of money management was just wonderful. I'd say the most important reading when you're starting out.

He clearly underlines, by how he tells the story (or history), that kelly is the guy who figured it all out, and, after him, a lot of academics and scholars have further explained and demonstrated how he had it right. He provides all the key readings and bibliography during and after his essay (or... post/note/webpage, I don't know what to call it anymore - at any rate it's as good as a Ph.D. thesis as far as I'm concerned).

Now, before I move on to study kelly's formulas (and all the bibliography he lists), I am going to do a lot more side activities to approach slowly the subject, because I am not ready for those formulas yet. Unfortunately there isn't a Khan Academy of formulas literacy, or on portfolio theory or on mathematical finance.

These side activies would be to first of all look at these, at the end of his essay:

Links

• money-management.pdf An exhaustive literature review on money management.
• money-management.php An online money management script.
• Kelly.xls An Excel spreadsheet implementation of the Kelly criterion, including an exponentially-weighted version which gives greater weight to more recent trades.

Man, Sewell website is gold, I'm telling you.

Done the checking out of the Links. In his history of money management, he says the father of all of this is Bernoulli. I like history so I'll check out Bernoulli first:
Exposition of a New Theory on the Measurement of Risk (translation by Louise Sommer). This is really cool, because Bernoulli cites works written 200 years later. Genius. This is going to be my next feat.

Amici miei - Carlo Rustichelli - YouTube

http://en.wikipedia.org/wiki/Carlo_Rustichelli