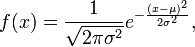my journal 2

[Yamato]

The meaning of "risk"

This is fascinating. It's like mental weight-lifting. You never want to do it, but if you do it, you start seeing improvements pretty quickly. In my case I wish it were like swimming, which i find enjoyable while useful to get into shape. Unfortunately, reading textbooks and formulas is not exactly as enjoyable and natural as swimming is for me.

So. I've been reading, Bernstein in particular. And the ideas I received started growing in my mind.

This time I'd like to talk about "risk".

When we talk about risk in finance, it means or at least it sounds like "risk of losing money". The way it always sounded to me was the "risk of losing money permanently", in other words "bankruptcy", "blowing out your account", "losing all your money".

Then I was reading Bernstein and his constant talk about stocks' superior return and for a second I said to myself: wait a minute, is "risk" just a synonym for "drawdown", "temporary loss of money"?

Yeah, because he kept saying (like many others do) that taking risks gets rewarded by a bigger return, and kept showing examples of how, overall, by investing in stocks you make more money, so one wonders if "risk" just means "drawdown".

But then I read about the "uncle fred" example, and it ends like this:
CHAPTER ONE

Uncle Fred’s coin toss may seem a most bizarre scenario, and yet it is nearly identical to the choice faced by most investors between the "safety" of money market accounts/treasury bills and the "gamble" of common stocks. The second option offers a near certainty of a superior result, yet comes at a price: the small possibility of an inferior result and, more importantly, that gut wrenching coin toss session with Uncle Fred each year. And yet, it is the 3% certificate of deposit option which is the most truly frightening—you will almost certainly live your golden years in poverty.

So, he's finally confirming to me, after going through dozens of pages, that "risk" isn't merely the "gut wrenching" part of variability in returns, but there is also a part where you "risk" not making as much money with bonds, and there is also a part where you "risk" losing everything, which is bigger with stocks than with bonds.

But then, if it is indeed like this, and there are no doubts that i am getting it right, he makes a mistake soon thereafter in chapter one:
CHAPTER ONE

where he says:

You have just been introduced to one of the fundamental laws of investing: in the long run you are compensated for bearing risk.

He should have said: "in the long run you are PROBABLY compensated for bearing risk EXCEPT when you lose everything".

The tradeoff between risk and return is of a nature whereby if you invest in one individual bond, you're actually risking more than if you're investing in 100 stocks.

First, because you will make less money, so we can say "you risk a lower return", given that the term "risk" is so abused anyway, let's mention all its aspects and implications.

Second, because the government (Argentina, for example) could go bankrupt and not pay you back, whereas a basket of stocks from all over the world would be safer.

So this is where I guess the "efficient frontier" (famous chart) comes into play. There's ways and ways to balance risk with return. You could invest in one bond and risk more than by investing in 10 stocks.

But yes, all other things being equal, a balanced portfolio of stocks yields more and implies a higher risk than a balanced portfolio of bonds.

And also, the longer term is your investment, just like tossing the coin, the more likely you are to benefit from stocks than from bonds.

So what these guys are saying, given the "uncle fred" example and all that, is that with stocks you are going to have a majority of profitable years, a minority of unprofitable years, and also the chance that during your lifetime you will be so unlucky as to lose... even everything. With bonds, you are going to have lower returns and pretty much the same exact thing, except the risk of losing everything is much lower, and the risk of not making any money is also lower.

So, all in all, we can say: in the long run there is a tendency to be compensated for bearing intelligent risk.

It is pretty far from what he said. But I'll keep reading his stuff nonetheless, and i owe him for his clarity.

But you see, we need to define once and for all this "risk" term, because it's still pissing me off.

How can one say "you're compensated for bearing risk in the long run"? That is contrary to any common sense interpretation of the word "risk". They don't really mean "take risks and you'll make money". What they mean is "if you diversify your portfolio and keep it for the long term, you will reduce your risks of losing everything so much and increase your probability of making much more money so much, that it will make sense to invest in stocks (or in a mix of stocks and bonds) rather than just bonds.

I am still not good enough to sum it up in a formula, but:

1) their concept of more "risk" does mean a higher risk of losing everything

2) but also their concept of more "risk" (despite the apparent contradiction) implies a higher probability of making money (with stocks)

So we're increasing the "risk" of a bad thing happening at a lower rate and at a lower speed than we're increasing the probability of a good thing happening.

So they should not make it sound like we're just increasing risk (of a bad thing). They should also stress out, each time, that we're increasing the probability of a good thing.

The problem with all their simplifications (bernstein's and markowitz's) is that they do not... not they... but the English and financial terms... they do not convey that we're not just increasing risk but we're also increasing the probability of a good outcome. So with this concept of doing something "risky" they make it impossible for any ignorant and superficial person like me to really grasp what the **** they might be talking about.

It's like the famous "no pain no gain"... I mean all this crap like "risk is rewarded"... this all sounds like "run to your death" and so obviously it doesn't make any sense to anyone who's unable to go beyond the appearance of words.

If you do so, you realize, you finally realize that what they are implying BUT NOT saying (the mother ****ers) is, as you accept a (slightly) higher risk of losing everything, if you are doing everything right and diversifying and holding for the long term, you will highly increase your probability of making a lot more money.

Goddamn mother ****ers.

Probably, because of the stupid journalists (because they're the ones spreading the superficial and dangerous bits of knowledge, here and there) the average moron will go to the bank and buy just argentinian bonds and feel secure. Then the other moron will also misinterpret it and go and buy a couple of stocks.

Anyway.

Another major point that Bernstein makes (but not in chapter one - nope he beats about the bush for several chapters) is that stock picking is useless. All that matters is a good balance of asset classes. The same thing more or less that markowitz seems to say.

Now, how does all this apply to my 120 systems?

Very much so, but let me think about it for a while.

Well, some brainstorming.

First of all, my trading systems would seem like a bunch of stocks, and they'll be even less correlated than stocks are. But then they might not be as good as all those asset classes that Bernstein cites (but in the other book, "The Investor's Manifesto"):

The first column simply lists the asset classes we are
examining; the first 12 of them are the major foreign and
domestic equity (that is, stock) classes, separated by three
different criteria: location (United States, foreign developed
nations, and foreign emerging - market nations), company
size (large versus small), and whether the companies
are of the “ value ” or “ market ” type.

Second of all, my systems are good enough to not need to be traded along with bonds in a diversified portfolio. By all means they will make money every single year.

Yes, as the "risk" term implies, there's a slightly higher risk that my systems will lose everything than if you simply bought a basket of bonds.

I haven't gotten so far as to read their recipe for diversification and limiting risk. But, once I do, I will have to learn their approach (and formulas) regarding how to avoid the pitfall of expecting a portfolio that was balanced in the past to necessarily work in the future. I will need to adapt such an approach to my systems. Whatever I do, this reasoning will help me, provided I get done with it. I can't leave this task unfinished or it will just make me more insecure with regard to math ("i tried again and failed again").

 

[Yamato]

Hackers: Wizards of the Electronic Age

Fascinating...

Hackers: Wizards of the Electronic Age - YouTube

 

[Yamato]

weekly update

My usual sad forward-testing. Sad because with no capital, but still fascinating. I am still forward-testing the combination of systems/contracts that exceeded our expected drawdown so much as to stop trading altogether.



Who knows. Maybe the combination touched bottom on the day we gave up. It looks that way so far. This was god telling me to stop trading with the investors, or the other way around. It doesn't matter: it was a bad over-optimized curve-fitted portfolio, regardless of what happens now. We shouldn't resume trading it even if we wanted to.

I am sad but also feel challenged. If I failed it just means I have to do better and try harder.

Hey, I finally found something to do which is more challenging than watching the cooking shows.

 

[megamuel]

Nobody seems to be commenting any more. Why is that?

 

[Yamato]

Well, this is unlikely the question that it seems to be, so it slightly pisses me off. I don't know if they're called "rhetorical questions" or something like that. Most likely you're pulling my leg, or rather: making a statement and saying... berating me because I scared the readers away. It's as if I asked you the question "Why are you an idiot?", which would not be a question but the equivalent of saying "you are an idiot". And it would be even more rhetorical and efficient if I formulated it like this: "may I ask you a question? why are you an idiot?", which would look like a polite question, whereas it's an insult. So, despite the fact that you're probably wasting my time with this "question", I am going to pretend it is a regular question, and answer it. I am going to pretend it is a regular question and you are interested in knowing my opinion.

Why are there no comments anymore? The way I see it is that they're not reading anymore either, except the usual few silent readers of mine. But you're right: how does a journal go from 10 comments per day to none at all... Maybe I got boring, or you would think that I banned them all, or that I threatened to ban you all. Maybe a little bit of both. The reason is that...

Maybe I got it. First: I discouraged comments, with various things I said and did (banning and complaining about people not reading my posts before asking questions). Then people stopped posting. Then, when people stop posting, and there's no debate, then most people also stop reading: I don't know if they're right or not, but they must find it less interesting. There is a tendency for most readers to be more interested in this journal when there is debate rather than where there isn't. Then if people stop reading, there's obviously an even lower chance of them posting, and the debate decreases even further, until it totally stops. So it's like a vicious circle that proceeds along these steps:

1) I got tired and discouraged comments
2) there were fewer comments
3) there were fewer readers
4) there were even fewer comments
5) there were even fewer readers... until discussion totally stops
6) ...but the readers do not go all the way to zero (cfr. what i write below)
7) then there's peace for a while, and I write in peace
8) but the few surviving readers still read and every once in a while one of them or a new reader will post a comment
9) occasionally from that comment, debate will spark again
10) occasionally I will get tired from replying to all posts, and will kill it all, all over again

But I am satisfied, because, despite there being no debate, 1) i am making more progress than when i was replying endlessly and 2) I know there's still a few selected readers reading me (my favorite ones: those who read without writing). That debate was mostly bull****, as people were often taking pages to write one good insight/question, and so it was 90% unnecessary hard work (answering the same questions over and over again, and hearing the same criticism over and over again).

Those rare insights were useful but overall it got to be so much work that it became counter-productive. You always need priorities. And I so had to kill the readers who were writing comments. It's like this lady with a child coming to my house: I might be able to have sex with her, but she's going to be so much of a burden (time and money) that I'd rather not even meet her. Damn. Instead she's coming (in two weeks), because one day I told her she's the woman of my dreams. Now I can't just say "I changed my mind, and I don't want to meet you". So, out of politeness I will host her, but then I will kill them in their sleep and dispose of their bodies, in the early morning, on Saturday. The priority in this case is to not offend people yet not waste too much time and money because of them. I was raised to be polite and I can't help it. But then, every once in a while, I have the split personality thing, like Jim Carrey in that movie:

IRENE YO Y MI OTRO YO (MEJORES ESCENAS) - YouTube


This is just the way i sound when I study mother ****ing math:

Me, Myself & Irene - Quantum Physics - YouTube

Actually, I am quite satisfied that no one is busting my balls any more with endless and repetitive questions. A journal is supposed to be a place where I write what I do, and hear some useful feedback, whereas here I was just breaking my back answering questions from people who were not reading my posts before asking their questions, and who, most likely, did not even read my answers afterwards. And then I even had to read a guy telling me that i was beating about the bush (!), when he hadn't even read my posts. And that was the last rhetorical question I took, too, because it's been a huge waste of time answering it. Pretty easy to spend 20 seconds to write... basically a question mark, and having me spend an hour answering your question mark. The next suspected rhetorical question or blatantly rhetorical question will be ignored.

How much power and how compelling a question mark is...

http://en.wikipedia.org/wiki/Question_mark

You guys have all fooled me for a month, with your question marks. Screw question marks. From now one no one can post any more question marks here, or if they do, I will ignore them. No more questions. No one is allowed to use the question mark. It's like an abuse. It's like a drug that makes me lose control and makes me start answering and work for hours and hours and it's just not worth it. No more question marks, or I'll interpret it as an insult, and ignore it.

 

[Yamato]

more bernstein: int.ass.allocator

Finishing chapter one, and doing some math exercises (attached, at the bottom of this post) as I read:
CHAPTER ONE

Now I got this far:

What does the standard deviation number actually mean? It means that two thirds of the time the annual return of the asset will lie between 1 standard deviation above and 1 standard deviation below the mean value. In the case of security A this means that two thirds of the time it will be between -1.46% (10 minus 11.46) and 21.46% (10 plus 11.46). I've graphed the "downside" for security A in Figure 1-2:

This shows that there is a 1 in 6 chance of a loss worse than 1.46%. There is a 1 in 44 chance of a loss worse than 12.92% (2 standard deviations less than the mean) and a 1 in 740 chance of a loss worse than 24.38% (3 standard deviations below the mean). To use a more simple example, let’s assume that you are considering a Latin American stock fund with an expected return of 15%, and a very high SD of 35%. This tells you to expect a loss of 20% or worse every 6 years, a loss of worse than 55% every 44 years, and a loss of 90% every 740 years. I very much doubt that many of the fund salesmen or brokers touting these funds in recent years conveyed such information to their clients. In fact, one sign of a dangerously overbought market is when there is a generalized underappreciation of the risks inherent in it.

I get what he says, but I don't get how he knows that if stdev is so and so for the past, we can expect the future to stay within those limits.

Normal distribution - Wikipedia, the free encyclopedia

In probability theory, the normal (or Gaussian) distribution is a continuous probability distribution that is often used as a first approximation to describe real-valued random variables that tend to cluster around a single mean value. The graph of the associated probability density function is "bell"-shaped, and is known as the Gaussian function or bell curve:[nb 1]

where parameter μ is the mean (location of the peak) and σ 2 is the variance (the measure of the width of the distribution). The distribution with μ = 0 and σ 2 = 1 is called the standard normal.
The normal distribution is considered the most prominent probability distribution in statistics. There are several reasons for this:[1] First, the normal distribution is very tractable analytically, that is, a large number of results involving this distribution can be derived in explicit form. Second, the normal distribution arises as the outcome of the central limit theorem, which states that under mild conditions the sum of a large number of random variables is distributed approximately normally. Finally, the "bell" shape of the normal distribution makes it a convenient choice for modelling a large variety of random variables encountered in practice.

Jesus, you mother ****ers, you really want me to get lost. Let's take a break and study this stuff on youtube or that other place that has the math videos.

Central limit theorem - Wikipedia, the free encyclopedia
http://en.wikipedia.org/wiki/Standard_normal_table

Damn. I don't get this one:
http://www.brightstorm.com/qna/question/10181/

Damn, I need to find videos now, and it seems I am back to algebra 2:
http://www.brightstorm.com/math/algebra-2/

http://www.brightstorm.com/math/algebra-2/combinatorics/introduction-to-probability/

Great teacher though.

Wow, this is just great. Here's another one:
http://www.educator.com/

This guy is a Ph.D.:
http://www.educator.com/mathematics/statistics/yates/

 

[megamuel]

You are banning question marks! It wasn't really rhetorical, as I don't know the answer. Although I have my theories - Most people find maths boring, as well as you seeing your ar$e with everyone. But, I thought it was an interesting point you made about that princess - When she was young and beautiful, everyone loved her. Now she's old and plastic and everyone takes the ****. It's like when you were trading big money everyone was interested but now you are trading on demo and talking about maths and nobody cares any more. Some tried taking the **** but you gave them a virtual b1tch slap! You seem to prefer it that way anyway.

As for me being an idiot, I don't know why. I guess it's a combination of genes, environment, alcohol, and not really having the desire/motivation to be an intellect. I like to know about what I need to know about, anything else to me is a waste of time really. Having said that, for my age group and location I am reasonably intelligent. Hell I live in Wales - Most people are retarded inbreds here. But I agree, in the big scheme of things I am an idiot, if I was in London for example I would be a complete cretin!

 

[Yamato]

Ok, then, luckily, I already took your question seriously (cfr.reply above), and I am glad it wasn't just a rhetorical question to blame me for scaring readers away. I apologize for accusing you of asking rhetorical questions. And I will keep you as a non-banned reader.

I think people got interested when I was losing, and were bored both before and maybe, as you suggest, after. But the biggest causes for no comments are still: 1) i discouraged comments, 2) comments decreased sharply, 3) readers decreased, 4) comments decreased even further.

Now I'll go back to studying math and watching these great videos:
http://www.brightstorm.com/math/algebra-2/

I am having to rediscover a language which I had archived, thinking I wouldn't need it anymore. Math and formulas are like a foreign language to me, something close to German: I only understand a little bit of it, and it bothers me. I am definitely not attracted to German, nor math.

 

[Yamato]

the mean, the median, the media and the L.A. Galaxy

Fascinating:
Statistical Median - Free Math Video by Brightstorm

Statistics is all about manipulating data to show what you want to show

Los Angeles Galaxy - Wikipedia, the free encyclopedia

Median - YouTube

2010 Los Angeles Galaxy Salaries - USATODAY.com

PLAYER    SALARY
David Beckham    *6,500,000
Landon Donovan    *2,127,777
Gregg Berhalter    *198,750
Edson Buddle    *188,488
Donovan Ricketts    *160,000
Omar Gonzalez    *157,000
Chris Birchall    *145,125
Dema Kovalenko    *144,118
Todd Dunivant    *126,750
Clint Mathis    *120,750
Israel Sesay    *107,083
Tristan Bowen    *101,363
Chris Klein    *                101,000
Eddie Lewis    *99,333
Mike Magee    *96,000
Alan Gordon    *87,731
Sean Franklin    *87,285
Jovan Kirovski    *84,000
Alex Dos S.Cazumba    *80,000
Juninho Gomes    *80,000
Leonardo R.Da Silva    *80,000
Josh Saunders    *60,608
AJ DeLaGarza    *45,100
Michael Stephens    *42,500
Bryan Jordan    *40,000
Yohance Marshall    *40,000

"...if there are an even number of values in the list, the median is the average of the middle two values". So the median here is 100,167. The average instead is 426,952. Yes, she has a good point! I would have been fooled. Almost everyone is making less than 200k per year, but the average salary is 400k. Yep, pretty good point.

Yeah, I am starting to like math. But I need to step up the pace or I won't ever finish what I need to cover.

Major sidetracking going on. If I keep going at this pace, I will never win the nobel prize for mathematics. I need to "buckle down", like Shonte Jr.

This is all about practice, just like any other language. I ain't stupid.

http://www.imdb.com/title/tt0183505/quotes

Shonte Jr.: Damn. I can't figure out the atomic mass of this mother****in' deuteron!
Jamaal: ****, man, that ****'s simple! Okay. Tell me this. Tell me this.
Shonte Jr.: What? What?
Jamaal: What's a deuteron made up of?
Shonte Jr.: Duh, a proton and a neutron.
Jamaal: Then what's this mother****in' electron doing right there?
Shonte Jr.: ****, I don't know!
Jamaal: Well, get it outta there then!
Shonte Jr.: Okay, so, you're sayin' I add up the atomic masses of the proton and the neutron, right, I see's that, but what do I do with the goddamn electron? Can I bring it over here?
Jamaal: Enrico Fermi'd roll over in his mother****ing grave if he heard that stupid ****. I mean, he'd just turn over ass up in your face. He wouldn't give a ****!
Lee Harvey: Hey, Jamaal, man, just cut my man some slack, dog.
Jamaal: Look here, man, I'm just tryin' to help him save face, all right? I mean, you know, he keep askin' questions like that, mother****ers gonna think he's stupid!
Shonte Jr.: I ain't stupid.
Jamaal: Aw, ****, man.
Charlie Baileygates: Mornin', fellas.
Lee Harvey: Oh, hey, Dad.
Jamaal: Hey, Pops, how you doin', man?
Charlie Baileygates: What's all the commotion down here?
Jamaal: Oh, you know, just school **** and ****.
Charlie Baileygates: How's my little guy doing?
Shonte Jr.: Struggling. This quantum physics is confusing. If I don't buckle down, I'm gonna get myself another B-plus.
Charlie Baileygates: Ooh, that'd be whack.
Lee Harvey: Man, he so ****in' dumb, he think calculus is a goddamn emperor.
Jamaal: [bumping fists] Give it up, dog.
Shonte Jr.: Yeah, well, you think polypeptide's a mother****in' toothpaste!

 

[Yamato]

The math muscles are building up... even if I had to do it by way of watching math videos, they're going to build up. This is a shortcut I cannot take. I am going to have to overcome my math problem.

Little by little, I will build up confidence, learn the language, get used to it... I will make progress. As long as I do not quit. And the amount of stuff to learn is not huge (basically it is all stuff that I should have studied in highschool).

It is not huge, but it needs to be done by me. It will not be done by itself. It will not be covered by my former classmates, it will not be done by my investors, whose skills were huge but unused, because they didn't apply them (I was taking care of everything). It has to be done by me. I have to overcome my phobia, and then overcome my ignorance. With the phobia, we're almost there, thanks to these videos I've been watching. It's almost gone. Then, with a more confident attitude, I will have to overcome my ignorance. By the way, all users writing posts that undermine my confidence will be immediately banned.

I have to be able to do it all myself: the systems, which are finished. The portfolio selection, which is a vacuum, and it was only apparently solved by the methods we used. In reality, being overwhelmed by data on the systems actually prevented us from looking at the right data, and prevented me... well, I was burned out, so I wasn't even alert as to what i was being told to do. Anyway, it's time for me to make the step of putting everything into my own hands.

It's irrelevant whether I won't have any capital for a year. This is going to take a while.

 

[Yamato]

statistical mode

I just watched this video:
Statistical Mode - Free Math Video by Brightstorm

I am learning about mode. Given that I am at the same time checking everything i learn on excel, I immediately thought: what if there are two modes?

Here's the answer:
Dealing with ties in the Mode Function - MrExcel Message Board

If there is a tie the Mode() function will return the first value it encountered... If you want multiple values you would probably need to make your own function.

Ha. It's kind of funny. I was thinking... if you don't understand german - and it's a foreign language for you - no one will tell you that you're stupid. They'll say "he's not stupid - he just didn't study german". But if you don't understand math, everyone kind of thinks that you're stupid. Including myself: I've always felt kind of stupid for not being good at math. The truth is that it's just like german. And if you had a bad german teacher, you'll feel you'll never be any good at german. Same with math. And, given that i spent most of my schooling years in italy, I had bad teachers for every single subject. They did not manage to fail me at everything. But they did manage to make me hate everything they were teaching me.

Let alone the help they got from my dad, in the task of making me hate school, since he was giving me extra homework, because he said i wasn't getting enough homework from school. Yeah, I have a sadistic father. I've said before. This is true: he was indeed giving me extra homework, ever since i was in elementary school. I was never good enough, and my grades were never good enough for him, so eventually I just quit studying and going to class. After a few years of that, he sent me to the states so I'd finish my education there. There it was easier.

In a way, what's kept me from doing well at school, and math, is my hate for my father. And my refusal to surrender and give in. What i am doing now is basically giving in and being a good boy. But being a good boy was never an option for me because there was no reward: it was just excel, excel and excel more. He never told me "good job". So he got me to quit. That was a very stupid coaching method. I wonder how he came up with that attitude. But i've seen people like that in movies: the great santini, and mr woodcock.

No, it's not the same actually. Math you studied all your life, so if you're not good, you end up blaming yourself, whereas if you didn't study german, you're not supposed to be good at it. So why do we not learn math... wait, but that is not even the case. The problem is not our lack of knowledge of it, but our insecurity with regard to it.

So, as soon as I restore that confidence that i once had (yes, because before i quit studying at 14, i was the first or second student in the math class), then most of the damage will be undone, and I will be able to pick it up from where i left it.

Yeah, because i am not missing that much stuff. It's just the confidence that i need, to fill up my ignorance. So I will keep on watching videos, and on reading all these simplified books.

Anyway, back to mode:
http://en.wikipedia.org/wiki/Mode_(statistics)

Excel does not work (but here there's a user-defined formula), but the wikipedia article is clear:

As noted above, the mode is not necessarily unique, since the probability mass function or probability density function may achieve its maximum value at several points x1, x2, etc.

The above definition tells us that only global maxima are modes. Slightly confusingly, when a probability density function has multiple local maxima it is common to refer to all of the local maxima as modes of the distribution. Such a continuous distribution is called multimodal (as opposed to unimodal).

Oh, and for excel 2010, they have a new mode.mult function:
http://office.microsoft.com/en-us/excel-help/mode-mult-function-HA010345299.aspx

Anyway, the mode function is not very important for excel, because you can easily find those values with a pivot table.

Now i will stop, because I won't push myself hard or there's a risk i'll quit like i did at 14, when mr woodcock was pushing me too hard.

I got here today:
http://www.brightstorm.com/math/algebra/introduction-to-statistics/mode-problem-1/

As long as I keep going and stay focused on math and portfolio theory, there is no rush.

 

[Yamato]

bernstein: "standard deviation is not good"

After spending a whole day studying it (and it still is not enough), it turns out that standard deviation, as i suspected (price is not random, and my systems are not random, and they're correlated), Bernstein tells me, at the end of chapter one, in smaller font, that standard deviation is no good:

OTHER MEASURES OF RISK

Those of you with sophisticated math backgrounds will recognize the limitations of SD as a measure of risk. For example, in the real world of investing, returns do not follow a classic "normal distribution," but instead more closely approximate a "lognormal" distribution. Further, there is a degree of asymmetry about the mean ("skew") as well as a somewhat higher frequency of events at the extremes of range ("kurtosis"). The most important criticism of standard deviation as a measure of risk is that...

Pretty wise, everything he says.

Important thing here:

There are nearly as many definitions of risk as there are finance academics.

Ok, done with chapter one, but now I need to investigate further on standard normal table.

 

[Yamato]

more bernstein's intelligent asset allocator

Before I forget: thanks to Liquid validity for his feedback on my previous post (in his recommendation).

Regarding Bernstein's book, instead, I had forgotten his foreword, which is pretty awesome:
FOREWORD

Here's a quote I appreciate:

4. Appreciate that diversified portfolios behave very differently than the individual assets in them, in much the same way that a cake tastes different from shortening, flour, butter, and sugar. This is called portfolio theory and is critical to your future success.

There's something more I want to discuss from chapter one:
http://www.efficientfrontier.com/BOOK/chapter1.htm

What do you do with a standard deviation? First and foremost, you should become familiar with this as a measure of risk. Typically, the standard deviation of the annual returns for various asset classes are as follows:

Money market (cash): 2%-3%

Short-term bond: 3%-5%

Long bond: 6%-8%

Domestic stocks (conservative): 10-14%

Domestic stocks (aggressive): 15%-25%

Foreign stocks: 15%-25%

Emerging Markets stocks: 25%-35%

I've finally digested the concept above (and what it leads to, a few lines later in the chapter), and i want to explain it out loud.

His reasoning is as follows and I also believe that it reflects the truth.

We have several asset classes: money market, bonds, stocks, and I'd add futures, too. Yeah, I am combining my understanding with his.

But then I won't just say "futures" but trading systems on futures.

Anyway. He says each asset class on average makes money, but, the more money it makes on average, the bigger is its standard deviation, and, up to here, this also applies to my trading systems.

Example: you put your money in the bank, and on average they give you 3%, and let's say, for the sake of simplicity, that the standard deviation is also +/- 3%. On average you make 3%, but you are likely to fluctuate higher or lower by 3%. The same applies to all other asset classes, and this so far makes sense. For example, with my systems, on average I make 100%, but also I might have a standard deviation of 100% -- all simplified, don't get me wrong.

So... I thought I was going to add something more, but maybe not. Oh yes. With his talk about 1 or 2 or more standard deviations, he also adds that, according to a normal distribution, you can make an estimate of the more rare outcomes for your capital depending on where you invested it.

Let's make a hypothesis. You invest in bonds and another one is that you invest in my trading systems on futures.

With bonds, the likely range is say 5%, and with my systems the likely range is 50%.

With his application of standard deviation he goes on and says, that with bonds, you will make 5% per year but on one sixth of the years, you will make nothing, and on another sixth of the years you will make 10%, and so on. And then he says that it's very unlikely that you will lose 90% of your capital on a given year. But there is still a possibility, even according to the normal distribution and all that.

Then with my systems, all this gets multiplied. Average profit gets multiplied by 10, and also the chance that you will lose everything is multiplied, It will not happen once in 200 years, but maybe once in 50 years.

On and on.

Another good point is that if you are not doing things right, things will radically change. Let's say you buy bonds from just one country, then things are different, because you're not diversifying. So you get to the point where investing in diversified futures is less risky and more rewarding than investing in non-diversified bonds.

These are just the ingredients. If I were to cook the recipe now, it would be pretty messy. But I am getting down the ingredients right now.

I still haven't got the recipe, I still am not ready to cook anything, but I am reasoning on the ingredients, and the quality of the ingredients. And this Bernstein seems to be a good cook.

 

[Yamato]

studying with kids

On this first web site (then on it, i found the link to the second web site) there's pictures of kids on the top. So much the better. It's going to be simpler:
Data, Probability and Statistics
Mathematics Quizzes

Fascinating how they explain to me the normal distribution:
Quincunx

And here's the best explanation of standard normal distribution i've come across so far. I had to come on a web site for teenagers to find it. Very good job.

Normal Distribution

I will continue tomorrow. The pills are kicking in.

Noir Désir - Le Vent Nous Portera - YouTube

 

[Yamato]

Muḥammad ibn Mūsā al-Khwārizmī

Fascinating sidetracking on math history:
Amu Darya - Wikipedia, the free encyclopedia

Abū ʿAbdallāh Muḥammad ibn Mūsā al-Khwārizmī[note 1], earlier transliterated as Algoritmi or Algaurizin, (c. 780, Khwārizm[2][4][5] – c. 850) was a Persian[1][2][3] mathematician, astronomer and geographer, a scholar in the House of Wisdom in Baghdad.
In the twelfth century, Latin translations of his work on the Indian numerals, introduced the decimal positional number system to the Western world.[5] His Compendious Book on Calculation by Completion and Balancing presented the first systematic solution of linear and quadratic equations in Arabic. In Renaissance Europe, he was considered the original inventor of algebra, although we now know that his work is based on older Indian or Greek sources.[6] He revised Ptolemy's Geography and wrote on astronomy and astrology.
Some words reflect the importance of al-Khwarizmi's contributions to mathematics. "Algebra" is derived from al-jabr, one of the two operations he used to solve quadratic equations. Algorism and algorithm stem from Algoritmi, the Latin form of his name.[7]

This is good, because I am making math mine, and I am hating it less and less. This is becoming something mine vs something that was forced into me, so much, that they made me reject it (my dad and the teachers). That mother ****er. I hope I'll get something back for having had such a terrible dad.

Anyway, can you believe it: this guy was called Mohammed Algorithm. You had to be good at math to be called Algorithm.

This historical overview cannot be complete without this link:
Timeline of mathematics - Wikipedia, the free encyclopedia

And this, too:
CCMR - Ask A Scientist!

Math wasn't invented in a day

Who invented math?
Ask your own question!

Math was not invented in one day or by some particular person. First people did observations and learned how to cope with everyday problems that might be called "mathematical" like counting (for keeping track of their domestic animals or doing trade), and learning to make different shapes (basket weaving, building shelters, and pottery). Very ancient animal bones with have been found in Africa and Europe containing notches made by human beings, who did some kind of keeping track of counts. These bones are believed to be between 8500 and 11,000 years old. Very old circular structures, which seem to be of astronomical significance, are found all over the world. Perhaps you have heard about Stonehenge in England, for example. This is where first knowledge in arithmetic and geometry comes from.

We do not know when, how, or why operations like addition or multiplication were invented, but they appeared several thousand years ago, apparently independently, in China, India, Mesopotamia, and Egypt. The oldest clay tablets with mathematics on it were found in Mesopotamia (nowadays Iraq) dating about 4000 years ago. The oldest written texts in mathematics - papyruses - come from Egypt, where civilization was already about 2000 years old when those papyruses were written. In ancient Sulba Sutras that come from India and are about 3500 years old one can find rules for building altars.

Among other things there is a famous theorem of Pythagoras about the sides of a right triangle. It is believed that Pythagoras was the first to prove this theorem - which means to answer the question of why this theorem is correct. That is why this fact is known as the Pythagoras theorem. This was happening in ancient Greece about 2500 years ago. From this time on there is a tradition in mathematics to always answer the question of why your result is true.

So, ok, math wasn't invented just by the Iraqis, but you know what I am getting at. The bush dick, bringing democracy to iraq, that was pretty ridiculous to begin with, even more now. He and the US media regarded them as some amazonian tribe...

 

[Yamato]

The history of Probability theory

This is going to be the branch I have to cover, so I might as well find out something about the history, which, as always, fascinates me:
Probability theory - Wikipedia, the free encyclopedia

History
The mathematical theory of probability has its roots in attempts to analyze games of chance by Gerolamo Cardano in the sixteenth century, and by Pierre de Fermat and Blaise Pascal in the seventeenth century (for example the "problem of points"). Christiaan Huygens published a book on the subject in 1657.[2]
Initially, probability theory mainly considered discrete events, and its methods were mainly combinatorial. Eventually, analytical considerations compelled the incorporation of continuous variables into the theory.
This culminated in modern probability theory, on foundations laid by Andrey Nikolaevich Kolmogorov. Kolmogorov combined the notion of sample space, introduced by Richard von Mises, and measure theory and presented his axiom system for probability theory in 1933. Fairly quickly this became the mostly undisputed axiomatic basis for modern probability theory but alternatives exist, in particular the adoption of finite rather than countable additivity by Bruno de Finetti.[3]

What is this thing "discrete" vs "continuous"?

Statistics: Discrete and Continuous Data - YouTube

Great. My ignorance keeps getting cured by the internet. It doesn't matter if I have to learn from children.

So, who are these guys?

Two Italians, the first and the last:
Gerolamo Cardano - Wikipedia, the free encyclopedia
Bruno de Finetti - Wikipedia, the free encyclopedia

http://www.probability.ca/jeff/ftpdir/mcfadyenreviews.pdf

Review of Liber De Ludo Aleae (Book on Games of Chance) by Gerolamo Cardano
1. Biographical Notes Concerning Cardano
Gerolamo Cardano (also referred to in the literature as Jerome Cardan), was born in Pavia, in present
day Italy, in 1501 and died at Rome in 1576. Educated at the universities of Pavia and Padua,
Cardano practised as a medical doctor from 1524 to 1550 in the village of Sacco and in Milan.
During this period he appears to have studied mathematics and other sciences. He published several
works on medicine and in 1545 published a text on algebra, the Ars Magna. Among his books is the
Liber de Ludo Aleae (Book on Games of Chance), written sometime in the mid 1500s, although
unpublished until 1663.

2. Review of De Ludo Aleae
Cardano’s text was originally published in Latin, in 1663. An English translation by Sydney Henry
Gould is provided in Professor Oystein Ore’s book Cardano, The Gambling Scholar (Princeton
University Press, 1953). Professor Ore’s book provides both biographical information relating to
Cardano, as well as commentary on Cardano’s presentation of a probability theory relating to dice
and card games.
In De Ludo Aleae Cardano provides both advice and a theoretical consideration of outcomes in dice
and card games. The text (as published) is composed of 32 short chapters. The present review is
concerned principally with chapters 9 to 15, illustrating aspects of the theory concerning dice.
The first eight chapters provide a brief commentary on games and gambling, offering advice to
players, and suggesting both the dangers and benefits in playing.

http://www.socsci.uci.edu/~bskyrms/bio/readings/EkertOnCardano.pdf

1. Gambling scholar
Girolamo Cardano, a 25 year old medical student from Padua, knew
the tricks of the trade and yet he was losing money at an alarming
rate. When he nally discovered that the cards were marked he did
not hesitate to draw his dagger. He stabbed the cheat in the face
and forced his way out of the gambling den into the narrow streets
of Venice, recovering his money on the way. Running for his life in
complete darkness he slipped and plunged into muddy waters of a
canal. Not the best place to be, especially if you cannot swim. It was
sheer luck that he managed, somehow, to grab the side of a passing
boat and get himself lifted to safety by a helpful hand. However, once
he regained his posture on the board, Cardano found himself facing
the man with a bandaged face, the same who had cheated him at the
gambling table few hours previously. Perhaps it was the chill of the
night that cooled the tempers or perhaps neither of the two wanted
trouble with the notoriously strict Venetian authorities, the fact is, there was no brawl. Instead,
Cardano was given clothing and travelled back to Padua in an agreeable company of his fellow
gambler...

Two French, from the 1600s:
Pierre de Fermat - Wikipedia, the free encyclopedia
Blaise Pascal - Wikipedia, the free encyclopedia

Mathematicians: Blaise Pascal - YouTube

It's clearer here:
The Story of Blaise Pascal

In 1654, a French nobleman, Chevalier de M�r�, challenged Pascal to solve a puzzle known at the time as the �problem of points�. The problem, first posed by an Italian monk in the late 1400s, had remained unsolved for nearly two hundred years. The issue in question was to decide how the stakes of a game of chance should be divided if that game were not completed for some reason. The example used in the original publication[1] referred to a game of �balla� where six goals were required to win the game. If the game ended normally, the winner would take all. But what if the game stopped when one player was in the lead by five goals to three?

In seeking a solution to the problem, Pascal entered into correspondence with the lawyer and mathematician Pierre de Fermat...

One dutch, also from the 1600s:
Christiaan Huygens - Wikipedia, the free encyclopedia

One Russian, 1900s:
Andrey Kolmogorov - Wikipedia, the free encyclopedia

One Austrian, 1900s, but born in a city that is now in Ucraine:
Richard von Mises - Wikipedia, the free encyclopedia

 

[Yamato]

taking a small break

I feel fine. I am covering the things I didn't cover in highschool. I feel no sorrow and I feel no shame.

It's funny because here they say the song is about marijuana:
http://www.songmeanings.net/songs/view/48918/

Quite a coincidence that there's a movie entirely about marijuana with Ed Norton, and he looks and talks like the lead singer:

Anyway, enough formulas for the day. I covered some more formulas. I am not entirely focusing on the subject but I am trying to make it more interesting for me and to approach it a little bit at a time. In the meanwhile I develop some knowledge on the subject, and I gain some confidence with formulas. It's working. I am getting used to math, despite the phobia I had developed as a teenager, due to my father overloading me with extra homework (on top of what I got from teachers).

Now I'll watch a movie.

Mother ****er. He made math hell for me. Instead of making it "fun" as they say: he made sure I got traumatized and hated it. Due to being the ****ing psychopath that he's always been. Only he's successful, so everyone admires him and praises him. Little does it matter that he's sicker than everyone else. Just like with adolf hitler: if you're sick and successful, you can become the leader of a nation and be called a genius, but then, if all of a sudden you're no longer sucessful, then you deserve death and you're mad. Such is the world.

 

[Yamato]

overwhelmed

I was going through a few of the many money management ebooks I had downloaded on emule when emule still worked efficiently (one year ago): e.p.chan, ralph vince and a couple more, and I felt discouraged.

First of all, every one of these is precisely a "book". And it is usually full of formulas. Now, I have decided that I will not go back to my ignorance and face formulas and math, and that is why I went back to studying math. But one thing is to say I will read formulas (and defeat my phobia), and another thing is to say that I will read the 400 pages of formulas by Ralph Vince in his book The Mathematics of Money Management. I mean: is it really necessary to write 400 pages? Could you not have summed it up in 10 pages?

Ralph, you were bored and had nothing better to do. Why don't you just admit it? And you wanted to overwhelm your readers, and discourage me in particular.

Instead today I will print chapter 6 from E.P.Chan's Quantitative Trading - How to Build Your Own Algorithmic Trading Business. He takes care of money management in one chapter.

Besides, Ralph Vince wrote 400 pages of formulas, but does he give us a place in his book where he describes clearly from the first to the last step everything you have to do for a good portfolio selection? Nope. Just like everyone else. They all spend hundreds of pages showing off their knowledge and formulas and no one addresses the problem clearly.

Everyone talks about Bernstein, and how clear he is, but he also, like everyone else, is busy getting famous and making history, and so he has to write a "book". Actually three books. Couldn't he just write one chapter? Is anyone familiar with "manuals"? No, because he has to first tell us the story of money, starting from the stone age. And if any of these ****ers wrote a 20-pages manual, he could not dedicate it to his wife.

Basically, what I am getting at is that all these mother ****ing academics will not get me to read their books, where they're busy showing off.

What I will do instead is learn the math I have to learn, thanks to targeted web searches, and proceed according to my own path, and, given that they don't explain clearly what to do anyway, I will have to reinvent the wheel and create my own formulas for portfolio selection. Then, after I am done, I might find my method mentioned in a book, but I am not likely to learn a method from these academics showing off. There's some who write to make money, and there's others who write to show off. There's very few who write to teach.

Actually math is a field where there is no bull****, but I am getting an idea that you can write bull**** even as formulas. But math is a language I have to learn. The problem will be applying the math I will learn to my portfolio selection. I have to do it by myself, given that the vendors write bull**** to make money, and the academic write bull**** to show off. And no one writes a clear and concise manual, because you can neither make money nor show off with it.

For example, here's chapter 2 from the very clear and concise (as everyone says in the feedbacks on amazon) Bernstein's book:

In the halcyon early summer of 1929, John J. Raskob, a senior financier at General Motors, granted an interview to Ladies Home Journal. The financial zeitgeist of the late 1920’s is engagingly reflected in a quote from...

Now, what the **** is the point of adding all this bull**** to a book? The point is being brilliant. The point is not being clear. The point is self-glorification. These mother ****ers are so busy being brilliant that they make us miss the point, and they take 10 times as much time to get to the point. They really really suck.

 

[Yamato]

what I have understood so far of Markowitz and Bernstein

Markowitz and his portfolio theory provide the formula for maximizing return given a level of risk, and minimizing risk given a level of return. And I intend "risk" as the probability of losing x money during a certain period of time.

Fascinating... this wikipedia entry says it all, and finally it is all clear to me:
Modern portfolio theory - Wikipedia, the free encyclopedia

Modern portfolio theory (MPT) is a theory of investment which attempts to maximize portfolio expected return for a given amount of portfolio risk, or equivalently minimize risk for a given level of expected return, by carefully choosing the proportions of various assets.

[...]

MPT is a mathematical formulation of the concept of diversification in investing, with the aim of selecting a collection of investment assets that has collectively lower risk than any individual asset. That this is possible can be seen intuitively because different types of assets often change in value in opposite ways.[2] For example, to the extent prices in the stock market move differently from prices in the bond market, a collection of both types of assets can in theory face lower overall risk than either individually. But diversification lowers risk even if assets' returns are not negatively correlated—indeed, even if they are positively correlated.

Bernstein, which came later, basically agrees, and he explains, with simple words, what "risk" means. As far chapter 1 and 2, and some other scattered stuff I read, he also says that, by diversifying, you can almost totally exclude the risk of bankrupt with stocks as well, and then, the only problem you're left with is the volatility of your investment. Basically Bernstein so far hasn't said anything that Markowitz and the others haven't said, but he has explained much more clearly to me.

Anyway, here's wikipedia once again:
William J. Bernstein - Wikipedia, the free encyclopedia

Bernstein is a proponent of the equity or index allocation school of thought, believing that all equity selection strategies should be focused on allocating between asset classes, rather than selecting individual stocks and bonds, or from the timing of their sales.

[...]

Bernstein is a proponent of modern portfolio theory, which stands in stark contrast to the view that skilled managers can succeed in picking particular investments that will outperform the market, whether through market timing, momentum investing, or finding assets whose future value have been underestimated by the market. He argues that the financial research literature shows that most return is determined by the asset allocation of the portfolio rather than by asset selection.

There you go: they're both on the same line. And...! How could i forget that Bernstein's web site is called:
http://www.efficientfrontier.com

What changes from them and me is that I do believe that you can pick the right trades, but this doesn't mean that I can't apply their portfolio theory formulas to selecting my systems. Or at least I hope it's that way, because so far they're making a lot of sense to me. Except for this part of course: "modern portfolio theory, which stands in stark contrast to the view that skilled managers can succeed in picking particular investments that will outperform the market". I definitely believe that I can outperform the market through technical analysis. But maybe I can apply their portfolio theory to my systems, and treat them as if they were asset classes.

 

[Yamato]

good links on markowitz

Modern Portfolio Theory Made Easy - Education Center - Yahoo! Finance

You can divide the history of investing in the United States into two periods: before and after 1952. That was the year that an economics student at the University of Chicago named Harry Markowitz published his doctoral thesis. His work was the beginning of what is now known as Modern Portfolio Theory. How important was Markowitz's paper? He received a Nobel Prize in economics in 1990 because of his research and its long-lasting effect on how investors approach investing today.

Markowitz starts out with the assumption that all investors would like to avoid risk whenever possible. He defines risk as a standard deviation of expected returns.

Rather than look at risk on an individual security level, Markowitz proposes that you measure the risk of an entire portfolio. When considering a security for your portfolio, don't base your decision on the amount of risk that carries with it. Instead, consider how that security contributes to the overall risk of your portfolio.

Markowitz then considers how all the investments in a portfolio can be expected to move together in price under the same circumstances. This is called "correlation," and it measures how much you can expect different securities or asset classes to change in price relative to each other.

For instance, high fuel prices might be good for oil companies, but bad for airlines who need to buy the fuel. As a result, you might expect that the stocks of companies in these two industries would often move in opposite directions. These two industries have a negative (or low) correlation. You'll get better diversification in your portfolio if you own one airline and one oil company, rather than two oil companies.

When you put all this together, it's entirely possible to build a portfolio that has much higher average return than the level of risk it contains. So when you build a diversified portfolio and spread out your investments by asset class, you're really just managing risk and return.

Markowitz Portfolio Selection - Selecting assets to meet a desired return at minimum variance.

(In the March, 1952, issue of Journal of Finance, Harry M. Markowitz published an article called "Portfolio Selection". In it, he demonstrated how to reduce the standard deviation of returns on asset portfolios by selecting assets which don't move in exactly the same ways. At the same time, he laid down some basic principles for establishing an advantageous relationship between risk and return, and his work is still in use forty years later.)

You're considering investing in three assets and historical data reveal that the return from each asset has fluctuated over time. You want to reduce variability, or risk, by spreading your investment over the three stocks.

From the historical data, you have calculated an expected return, the variance of the return rate, and the covariance of the return between the different assets. Variance is a measure of the fluctuation in the return - the higher the variance, the riskier the investment. The covariance is a measure of the correlation of return fluctuations of one stock with the fluctuations of another. High covariance indicates that an increase in one stock's return is likely to correspond to an increase in the other. A low covariance means the return rates are relatively independent and a negative covariance means that an increase in one stock's return is likely to correspond to a decrease in the other.

You have a target return of 15%. What percentages of your funds should you invest in each of the three assets to achieve this target and minimise the variance (or risk) of the portfolio? As an additional safety feature, you decide to invest no more than 75% in any single asset.

The objective is to determine the percent to invest in each asset while minimising risk of the entire portfolio...

The first link is really good. I used red font for the parts I liked the most.