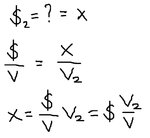eureka
Wow, this is a good one. I woke up with this idea and I don't think it can be wrong.
Ok, so I take the whole back-tested relativized equity line, with today's prices (I downloaded them a few months ago, but they're still close).
Then I start with the capital of 4000 that I will have and I run several tests, whereby I hop on that equity line on random dates, starting on day one and ending one year before the equity line ends. Then I see how it goes, and I will know, according to the past, how likely I am to blow out or otherwise.
This is not going to be as quick to implement as it sounds, but it's clear what I have to do.
Oh, another thing: if at any time after hopping on the equity line, I fall below 2000 dollars, then that's clearly the moment I blow out. Otherwise I keep it going.
I don't know if this is called montecarlo testing, but I am going to pretend that's what it is. Or I could call it monte-cazzo testing, because it's a bit crappy, but it's the closest thing to science that I can afford right now, with my limited skills.
From:
Monte Carlo methods in finance - Wikipedia, the free encyclopedia
which took it from:
Financial Mathematics Glossary K-O
The Monte Carlo method, encompasses any technique of statistical sampling employed to approximate solutions to quantitative problems.
Ok, here's the file. I will attach it here, but then I'll do it from work, because otherwise I'd have to go late to work:
View attachment MonteCazzo_Simulation.xls
Ok, a few more things.
1. Given that there's already a bias, from the fact that we can only choose what works, and what works today is not likely to work as well in the future, almost by definition. But we can't do anything about this. However, what I will not do is include the forward-tested period, because that's even more bias, because i chose the systems to trade based on that period.
2. I will poll the whole population of data, so I am not "sampling", at least from the little statistics I studied. So this should be called anything but "MonteCazzo sampling".
3. I will use every part of the population, because even though of course you can't blow out if you started trading yesterday, this probability of not blowing out will be compensated by a lower profit, which I will also measure. If anything I'll get rid of the last period (where you can't blow out) at the end.
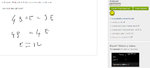
I've thought about this, while I was in the bathtub. I will have two columns, indicating the lowest and highest balance reached after starting at any given point. The first cell will indicate what's your lowest point if you hop on the equity line right there, on that specific date, and another cell will indicate what you will reach at your highest. But that second column might not even matter so I could remove it. Unless I want to do a ratio between the two.
Then I will say that if your lowest point is below -2000, that means you blow out, because I start with a capital of 4000 and IB doesn't let you trade unless you have at least 2000 on the account (the margin I need instead is lower than that).
[...]
Back at the office.
So here's the situation. This is close to a maximum drawdown calculation, but not the same thing, and we can say that what I have to do has not much to do with monte carlo simulation, not that I really know what it means anyway. Nonetheless there's still some element of randomness in my concept here, even though I can't define it exactly, being a math beginner.
So let's exemplify it. If this is the equity table:
+1
+3
-3
-2
+1
-2
+10
The maximum drawdown concept would say that the max drawdown is -6 on the penultimate trade, and that when the +10 trade happens, everything is reset to a drawdown of zero.
However what i need is different, as i said. Let's say those seven trades are my whole data. In reality I have 800 trades, or rather 800 equity days, because I measure by day, and some days there's more than one trade. But let's say I only have those seven days (each element is not a "trade", as I said earlier, but a "day").
So what I want to do is to see what would happen if I hopped on the portfolio equity line on day 1, 2, 3, 4, 5, 6, 7, which I will list again:
+1
+3
-3
-2
+1
-2
+10
The drawdown would only tell me that if I hop on the worst day, I go down -6. So, as I said earlier, I know how much margin I would need (if the past repeated itself) to be safe, and I've already said that I don't got the 8k I'd need (if the past repeated itself). So I know I am taking a risk, but I want to know how probable, and drawdown doesn't do it, because it just tells me the extent of the risk on the worst day, but not the frequency of that risk.
Let's list them one more time:
+1
+3
-3
-2
+1
-2
+10
If I hop on day one, the formula I have to devise on excel would have to tell me that, starting on that day, I can only go down... 1+3-3-2+1-2+10... -2. And what I used is the sum... the running total of the elements. And I get its lowest value, and that is what I need. But I want to have everything on one cell, rather than having an entire column per element, given that there's going to be hundreds of elements. I'm going to try this directly on excel.
[...]
...still working on it... this is really complex for my small brain... but i really need and can and will get to the bottom of this... furthermore today that my idiot colleague isn't here and I can still focus... this is something between the running total and the maximum drawdown with a pinch of array-entered formulas...
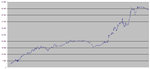
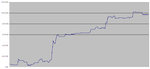
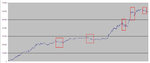
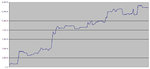
Ok, a chart might help:
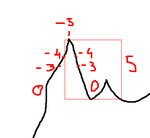
When I have a drawdown of -5, what I am really told is that I would have lost 5 had I started trading precisely on the day at the peak of that chart. If I had started one day earlier, I would have lost 4 (by first making one and then losing it), and if I had started one day later I would have lost 4. And so on. So, among the other things, this is very reassuring, because it's telling me that the drawdown happens as it did in the past only if you happen to start on that day. So, it doesn't matter that in 10 years you've had a drawdown of 10k. (If the past repeats itself) that 10k drawdown will only happen if you start trading on the worst day of the next 10 years. Or if you keep on increasing the futures traded, which I will not do. Yes, because by ever increasing your futures traded it is as if you started trading every day.
But then of course, I don't only have to worry about starting to trade on that peak, because it's not like I have 10k and have to worry ONLY about not starting in a situation where I can lose >8000. I also have to worry about starting one day before or one day after, and so on. I have to worry about the drawdown of 7000, of 6000, of 5000, and so on.
All right. For sure it won't hurt to set up my database with the running total on a column and the drawdown on another but then also the "draw-up" and see how I can make them interact to come up with what I need.
[...]
No, wait. Maybe I don't need the "draw-up". Here's what I need:
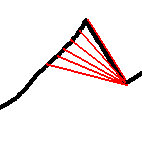
The equity line is represented by the pivot table's "running total" function. Now I simply need the distance between the lowest level of the running total column AFTER the date I poll, and I need to subtract this value from the running total of the element polled. That way we can figure out how much we fall from each point of the equity line. So, I might be able to figure this out. This time the math I studied helped, because cartesian geometry made me understand a little better the correspondence between equations and graphs, and that sometimes something you don't grasp in an equation you can grasp from a chart.
[...]
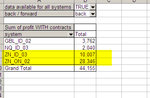
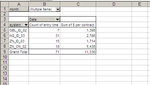
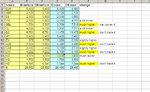
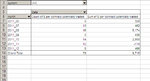
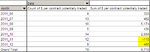
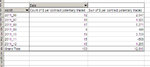
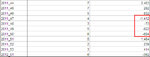
Ok, I am getting there... Here's the columns I created and what they do:
date: the date of the day when 1 or more trades took place
daily profit: total profit (or loss) made during the day
running total: sum of previous daily profits (or losses) up to that point
lowest subsequent running total: what is the lowest subsequent point of the running total
fall between now and then: it subtracts the lowest subsquent value from the point we're at right now, and tells us what would happen to our equity if we started trading the portfolio AFTER today's trades closed (always assuming the past repeated itself).
drawdown: this is only for double-checking purposes and it makes sure that the biggest fall measure with one method corresponds to the biggest fall measure with the other method. The problem with drawdown and why I could not use it is that it is sort of a "running total of the falls", but it doesn't tell me the subsequent max fall at each spot of the equity line (cfr. charts shown above).
Probably I could have derived everything from the drawdown, but I am not smart enough to do it.
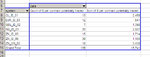
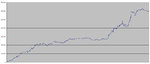
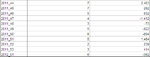
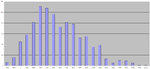
Here is the resulting chart, of the falls from the portfolio:
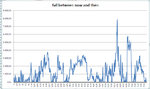
But a table with percentage is clearer in this case. This chart gives the mistaken idea that I am often above a risk of several thousands in losses, whereas, if you started trading on a random day of the back-tested period, the percentage of days where I'd blow out the account is lower than it looks on the chart.
I renamed the file from MonteCazzo_Simulation.xls to risk_of_ruin_tests.xls, which is more serious a name, for a better job:
View attachment risk_of_ruin_tests.xls
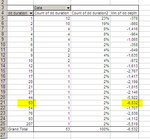
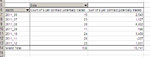
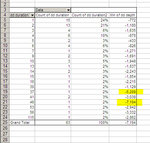
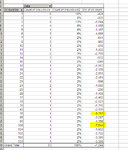
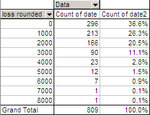
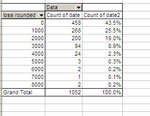
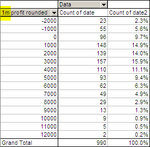
And here's the summary table:
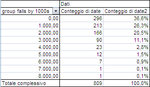
So basically, if the past repeated itself, by starting on a random day, with a capital of 4000 dollars, I would have a risk of about 17% of blowing out my account, a probability of 37% of not seeing any drawdown (or less than 500, since the grouping was done by rounding to the nearest thousand). I would have two chances out of three of not seeing any relevant drawdown (less than 1500).
But this is provided that I neither change the portfolio (by let's say doubling up the contracts) nor withdraw money from the account. Because in that case, if I withdrew 1000 dollars, any loss of 1000 (depending also on when it happened) would become a loss of 2000 (1000 withdrawn from the market and 1000 withdrawn from me).
At the same time, given the knowledge that the maximum fall (both according to max drawdown and to this formula I used) is 8000 dollars, I know that if I ever reach a capital of 10k, then suddenly it becomes unlikely that my withdrawing money will cause me to blow out the account. But this short-circuiting my brain, so I can't bring it any further. There's too many things involved and I can't figure out this estimate. But I would be satisfied if the estimate I've done is correct (provided that the past repeated itself, which it doesn't and, also, it is not random).
I also tried to remove the last year, to make sure that the fact that not much time had elapsed would not decrease the probability of blowing out. It didn't make much difference. For now this is enough. I don't want to do too much and make a bunch of mistakes.
I am satisfied with this work and with the results. The third and final version is a .zip file, at the bottom of this post.