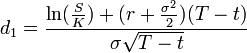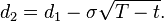Hi Guys,
Could anyone tell me how I would work out the % chance of a stock being above/below a price by DEC expiration given some number for volatility?
More specifically, a stock is currently trading at 84.80 and its 90Call option has an IV of 44.50. So if anyone could help me calculate what I stated above in this situation, I would greatly appreciate it.
Thanks for your help.
Could anyone tell me how I would work out the % chance of a stock being above/below a price by DEC expiration given some number for volatility?
More specifically, a stock is currently trading at 84.80 and its 90Call option has an IV of 44.50. So if anyone could help me calculate what I stated above in this situation, I would greatly appreciate it.
Thanks for your help.