I shall expand a little - though I shall let it be known now that this is pushing the boundaries of any practical understanding I have!
In the first instance, I think it is important to establish the conditions under which said spread is to be traded; Arabian, if you are looking to trade the spread in the same manner as a prop trader might trade a STIR spread (that is, over short timeframes, using the balance of bids to offers, and reactions to economic announcements', to determine your positions), what follows may not be of much use to you.
(it may all be bulls!t anyway).
Now, moving on to explain the context in which I suggested the spread might be "mean reverting"...
1) LET us consider, briefly, the macroeconomic factors that drive the prices on bonds, and subsequently their futures. We have Interest rates; Inflation; Growth to begin with. This is true for both European and British debt instruments (and all FI over the world...)
2) IT could be argued that the specifics of these contributors do not differ much, if at all, between Europe and GB - (one might argue that GB is a little farther down the stagflationary route, but europe is soon to follow) - Despite the different labels they fall under (exclude currency risk for simplicity), they are very much subject to similar pressures; "A Gilt-Edged bond by any other name would smell as sweet"...
3) HAVING established that the two prices are expected to behave in very similar ways, it is natural to examine the difference between the two. Moreover, it should be possible to establish a limit whereby the difference between the two contracts is above/below that which can be reasonably expected, given the similar driving factors of price - it follows that there should be some range of differences, whereby a "spread" breaching said range offers an opportunity for "pseudo arbitrage"...
[I will take a minute to draw an analogy; Consider the TED spread - the difference between a bond underwritten by the US Treasury, and the interest available over an identical term through a Aaa rated bank at the LIBOR rate. The difference between the two represents the confidence in creditworthiness of US Treasury over the Aaa rated banks - one is a Risk-Free rate, the other is the LIBOR. There will come a point where the implied creditworthiness of the LIBOR rate is sufficiently over/under priced compared to the genuine credit risk - a pertinent example given events over the last 18 months. It may have been possible to lend to an Aa institution at a Baa rate, for example - funded by the correctly measured (or at least, less incorrect) Risk Free rate from the US Treasury. *Moody's notation*
This is of particular relevance given that the consumer has little skill in correctly determining the creditworthiness of a Bank (e.g. Northern Rock); the LIBOR contributors were aware of this, so they lied. The LIBOR fiasco continues, although on friday the BBA said they weren't going to change the measurement all that much.]
In the context of the Bund - Gilt spread, I mean to say the following: Given the similarities of the Inflation, Interest rate and Growth contributors, ceteris paribus, the two contracts should behave in the same way; Furthermore: if, say, the change in price of the Gilt contract due to inflation expectations was far removed from it's Bund counterpart - ceteris paribus - the opportunity would exist to construct a portfolio that hedged out the Interest rate and Growth risk, leaving a portfolio Long/Short "Gilt Inflation Delta" - a portfolio that would collect profit as the two indflation expectations aligned themselves.
There will exist a boundary whereby the differences in the priced-in Inflation expectation between the Bund contract vs. the Gilt contract are fundamentally reasonable; beyond that, a portfolio similar to that described above could be constructed to generate "pseudo arbitrage". So where I say "mean reverting", perhaps "range bound" is more appropriate.
Moving from a fundamental to quantitative analysis of the spread (I shall breeze over the "long on the spread because it's at a fib retracement" argument); Interest rates are frequently given the "mean reverting random walk" treatment - ergo I see no reason why the spread should be any different. Given a spread outside of the likely range, it follows that the priced-in interest rates of (at least) one of the two contracts - again, ceteris paribus - are beyond that which can be quantitavely explained. The requirements to trade the spread quantitavely are beyond me - but well within the means of some rocket scientist on a quant arb. desk; thus, we should expect the spread to behave as the quants expect it - as a mean reverting stochastic variable.
RE: Pull to Par - Grant, here you make an interesting point. Perhaps there does exist a trade that would hedge out the Inflation, Interest rate and Growth conributors, and profit from a differential between the "acceleration" of PTP the two cash bonds were demonstrating (ceteris paribus, of course). Although I must say that I think a trade that is so obvious would be priced into said cash bonds - and futures - and eliminate any opportunity for profit.
[No offence mate; i just think it's too obvious not to be priced in]
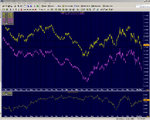
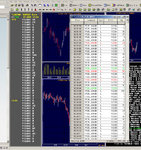
To conclude: these are the reasons why I mentioned the "mean reverting" statement. Grant(ed), "mean reversion" might be wholly inappropriate, but I hope to have explained why the "range bound" argument - what I meant to say initially - holds some firmer ground. Of course, 90% of what I say is b0llocks anyway, as consolation I attach the following documents: A chart of front month Bund future (yellow), the front month Gilt future (purple), and the spread between the two (shown below). I also attach a 365 trading day history of said contracts, for you to do with as you wish.
p.s. since starting to reply, I have polished off a bottle of 2004 cotes du rhone.
p.p.s. The excel sheet uses my DDE; choose "don't update" or it'll c0ck up.